Graphic system of equations. Graphical solution of systems of linear equations
Graphical way solutions of systems of equations
(9th grade)
Textbook: Algebra, Grade 9, edited by Telyakovsky S.A.
Type of lesson: a lesson in the complex application of knowledge, skills, abilities.
Lesson Objectives:
Educational: Develop the ability to independently apply knowledge in a complex, transfer it to new conditions, including working with a computer program for plotting function graphs and finding the number of roots in given equations.
Educational: To form students' ability to highlight the main features, establish similarities and differences. Enrich vocabulary. Develop speech, complicating its semantic function. Develop logical thinking, cognitive interest, culture of graphic construction, memory, curiosity.
Educational: Cultivate a sense of responsibility for the result of their work. Learn to empathize with the successes and failures of classmates.
Means of education : computer, multimedia projector, handout.
Lesson plan:
Organizing time. Homework- 2 minutes.
Actualization, repetition, correction of knowledge - 8 min.
Learning new material - 10 min.
Practical work - 20 min.
Summing up - 4 min.
Reflection - 1 min.
DURING THE CLASSES
Organizational moment - 2 min.
Hello guys! Today's lesson important topic: "Solution of systems of equations".
There are no such areas of knowledge in the exact sciences, wherever this topic is applied. The epigraph to our lesson is the following words : "The mind is not only in knowledge, but also in the ability to apply knowledge in practice ". (Aristotle)
Setting the topic, goals and objectives of the lesson.
The teacher informs the class about what will be studied in the lesson and sets the task to learn how to solve systems of equations with two variables in a graphical way.
Homework (P.18 No. 416, 418, 419 a).
Repetition theoretical material– 8 min.
BUT) Mathematic teacher: According to the finished drawings, answer the questions and justify your answer.
1). Find Graph quadratic function D=0 (Students answer the question and name graph 3c).
2). Find a graph of an inversely proportional function for k > 0 (Students answer the question, call graph 3a ).
3). Find a graph of a circle with center O(-1; -5). (Students answer the question, call graph 1b).
4). Find the graph of the function y =3x -2. (Students answer the question and name graph 3b).
5). Find the graph of a quadratic function D >0, a >0. (Students answer the question and name graph 1a ).
Mathematic teacher: – In order to successfully solve systems of equations, let's remember:
one). What is a system of equations? (A system of equations is called several equations for which it is required to find the values of the unknowns that simultaneously satisfy all these equations).
2). What does it mean to solve a system of equations? (To solve a system of equations means to find all solutions or to prove that there are no solutions).
3). What is the solution of a system of equations? (The solution of a system of equations is a pair of numbers (x; y), in which all the equations of the system turn into true equalities).
4) Find out if the solution of the system of equations 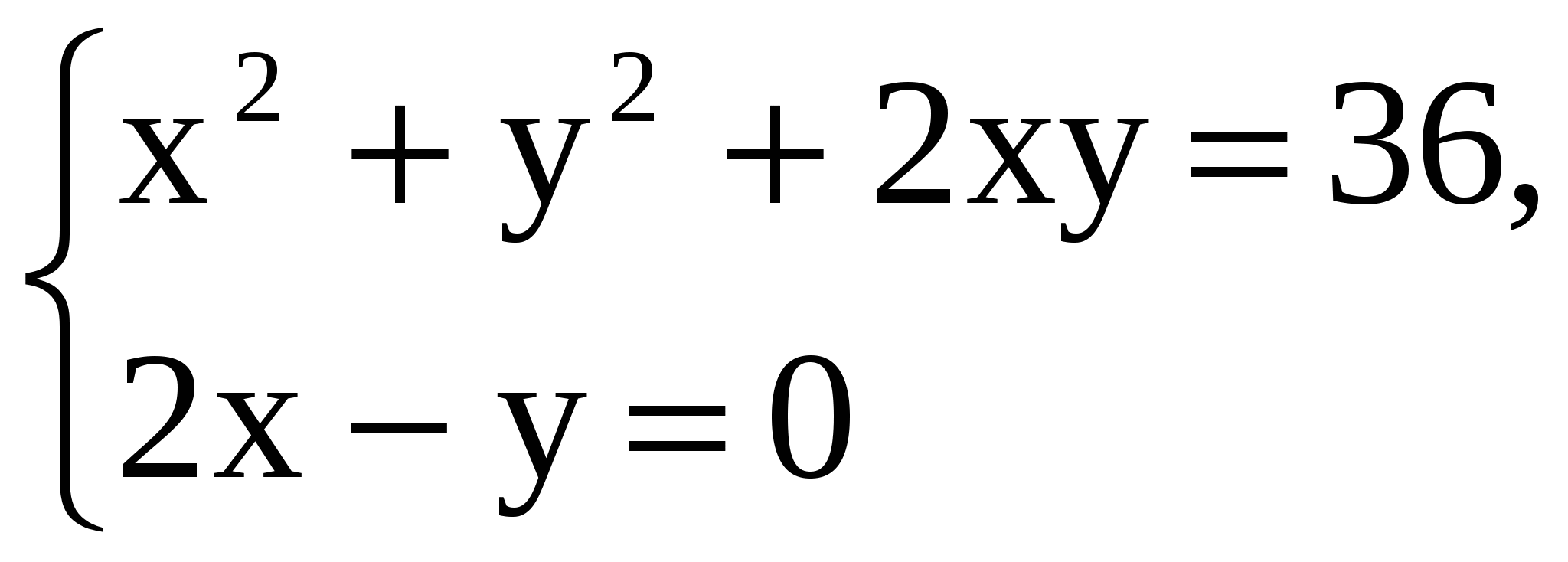 pair of numbers: a) x = 1, y = 2;(–)
b) x = 2, y = 4; (+)
c) x \u003d - 2, y \u003d - 4? (+)
pair of numbers: a) x = 1, y = 2;(–)
b) x = 2, y = 4; (+)
c) x \u003d - 2, y \u003d - 4? (+)
III new material- 10 min.
Item 18 of the textbook is presented by the method of conversation.
Mathematic teacher: In the 7th grade algebra course, we considered systems of equations of the first degree. Now let's deal with the solution of systems composed of equations of the first and second degree.
1. What is called a system of equations?
2. What does it mean to solve a system of equations?
We know that the algebraic method allows you to find exact solutions to the system, and the graphical method allows you to visually see how many roots the system has and find them approximately. Therefore, we will continue to learn how to solve systems of equations of the second degree in the next lessons, and today the main goal of the lesson will be practical use computer program for plotting function graphs and finding the number of roots of systems of equations.
IV . Practical work - 20 min. Solving systems of equations graphically. Determination of the roots of equations.(Plotting a graph on a computer.)
Assignments are completed by students on computers. Solutions are checked during operation.
y=2x2+5x+3
y=4
y \u003d -2x 2 + 5x + 3
y=-3x+4
y = -2x2 -5x-3
y=-4+2x
y=4x2+5x+3
y=2
y= -4 x 2 +5x+3
y=-3x+2
y = -4x2 -5x-3
y=-2+2x
y = 4 x 2 + 5 x+5
y=3
y = -4x2 +5x+5
y=-x+3
y = -4x2 -5x-5
y=-2+3x
Here are the graphs of two equations. Write down the system defined by these equations and its solution.








– Which of the following systems can you solve with this picture?


– 4 systems were given, they had to be correlated with the graphs. Now the task is reversed: there is charts, they need to be correlated with the system.

Summing up the lesson. Grading - 4 min.
* Solving systems of equations. ( Tasks with an asterisk*.)
Equations for the 1st group of students:
Equations for the 2nd group of students:
Equations for the 3rd group of students:
x y = 6
x 2 + y = 4
x 2 + y = 3
x - y + 1= 0
x 2 - y = 3
One way to solve equations is a graphical method. It is based on plotting functions and determining their intersection points. Consider a graphical way to solve the quadratic equation a*x^2+b*x+c=0.
First way to solve
Let's transform the equation a*x^2+b*x+c=0 to the form a*x^2 =-b*x-c. We build graphs of two functions y= a*x^2 (parabola) and y=-b*x-c (straight line). Looking for intersection points. The abscissas of the intersection points will be the solution to the equation.
Let's show with an example: solve the equation x^2-2*x-3=0.
Let's transform it into x^2 =2*x+3. We build graphs of functions y= x^2 and y=2*x+3 in one coordinate system.
Graphs intersect at two points. Their abscissas will be the roots of our equation.
Formula solution
To be convincing, we check this solution analytically. We will decide quadratic equation according to the formula:
D = 4-4*1*(-3) = 16.
X1= (2+4)/2*1 = 3.
X2 = (2-4)/2*1 = -1.
Means, solutions match.
The graphical method of solving equations also has its drawback, with the help of it it is not always possible to obtain an exact solution of the equation. Let's try to solve the equation x^2=3+x.
Let's build a parabola y=x^2 and a straight line y=3+x in the same coordinate system.

Again got a similar picture. A line and a parabola intersect at two points. But we cannot say the exact values of the abscissas of these points, only approximate ones: x≈-1.3 x≈2.3.
If we are satisfied with the answers of such accuracy, then we can use this method, but this rarely happens. Usually exact solutions are needed. Therefore, the graphical method is rarely used, and mainly to check existing solutions.
Need help with your studies?

Previous topic:
ALGEBRA 9 CLASS
Graphical way
solutions of systems of equations

1. Find on the schedule:
a) zeros of the function;
b) range of function values;
c) intervals of increase and decrease of the function;
c) intervals in which y ≤ 0, y ≥ 0.
d ) the smallest value of the function.

1.From the proposed formulas, select the formula
which defines the function presented on the graph
a ) y \u003d - 3x + 1; b) y \u003d 2x + 1;
c) y \u003d 3x + 1 .

From the suggested formulas, choose the formula that
defines the function presented on the chart
b) y = - 2x 2 ; c) y = x 2 +1.
a) y = x 2 ;

From the proposed formulas, select the formula that defines the function presented on the graph.
b) y \u003d 2 x 3; c) y \u003d x 3
a) y \u003d 0.5x 3;

From the proposed formulas, select the formula that defines the function presented on the graph
a) y \u003d 4 / x; b) y \u003d - 4 / x;

Linear equation with
one variable
ax=b
- Linear equation with
two variables

Equation with two variables
The graph of an equation with two variables is a set of points of the coordinate plane, the coordinates of which turn the equation into the correct equality

The equation
We express y in terms of x
3x+2y=6
2y-x 2 =0
This formula defines....
Serves as a schedule
2x+y=0
hyperbola
quadratic
function
y \u003d -1.5x + 3
Linear
function
straight
y=0.5 x 2
reverse
proportionality
y= -2x
parabola
straight, right
through the beginning coord.
straight
proportionality

Ellipse

X 2 y \u003d 4 (2-y),
y=8 /(x 2 +4)


System of equations and its solution
Definitions
- A system of equations is a number of equations, united by a curly bracket. The curly brace means that all equations must be executed at the same time
- A solution to a system of equations with two variables is a pair of values of variables that turns each equation of the system into the correct equality
- To solve a system of equations means to find all its solutions or to establish that there are none.

Way
substitutions
Way
additions

Methods for solving systems of equations
Way
substitutions
Way
additions

Graphical way
solutions of systems of equations

1. Express y through x in each equation.
2.Build a graph in one coordinate system
each equation.
3. Express y through x in each equation.
4.Build a graph in one coordinate system
each equation
5. Determine the coordinates of the intersection point
graphs.
6. Write down the answer: x = ...; y \u003d ..., or (x; y)

System solution graphically
Express y
Let's build a graph
first equation
Let's plot the second
equations -circle with
centered at the point O(0;0) and
radius 2.

System solution graphically
Express y
Let's build a graph
first equation
Let's plot the second
equations -circle with
centered at the point O(0;0) and
radius 2.
X 2 +y 2 =4*
The system has 2 solutions:
Answer: (0;2), (-2;0)

1. We start charging,
We stretch our hands
We stretch the back, shoulders,
To make it easier for us to sit
2. We twist-turn our heads.
Stretch your neck, stop!
One, two, three - tilt to the right,
One, two, three - now to the left.
3. Now stop!
Raise our hands higher
Inhale and exhale. We breathe deeper.
Now let's sit down at the desk.
Consider the following equations:
1. 2*x + 3*y = 15;
2. x2 + y2 = 4;
4. 5*x 3 + y 2 = 8.
Each of the above equations is an equation with two variables. The set of points on the coordinate plane whose coordinates turn the equation into a true numerical equality is called graph of an equation in two unknowns.
Graph of an equation with two variables
Equations with two variables have a wide variety of plots. For example, for the equation 2*x + 3*y = 15, the graph will be a straight line, for the equation x 2 + y 2 = 4, the graph will be a circle with a radius of 2, the graph of the equation y*x = 1 will be a hyperbola, etc.
Integer equations with two variables also have such a thing as a degree. This degree is determined in the same way as for the whole equation with one variable. To do this, the equation is brought to the form when the left side is a polynomial of the standard form, and the right side is zero. This is done through equivalent transformations.
Graphical way to solve systems of equations
Let's figure out how to solve systems of equations that will consist of two equations with two variables. Consider a graphical way to solve such systems.
Example 1. Solve the system of equations:
( x 2 + y 2 = 25
(y = -x 2 + 2*x + 5.
Let's plot the graphs of the first and second equations in the same coordinate system. The graph of the first equation will be a circle centered at the origin and radius 5. The graph of the second equation will be a parabola with branches down.
All points of the graphs will each satisfy their own equation. We need to find such points that will satisfy both the first and second equations. Obviously, these will be the points where these two graphs intersect.
Using our drawing, we find the approximate values of the coordinates at which these points intersect. We get the following results:
A(-2.2;-4.5), B(0;5), C(2.2;4.5), D(4,-3).
So our system of equations has four solutions.
x1 ≈ -2.2; y1 ≈ -4.5;
x2 ≈ 0; y2 ≈ 5;
x3 ≈ 2.2; y3 ≈ 4.5;
x4 ≈ 4,y4 ≈ -3.
If we substitute these values into the equations of our system, we can see that the first and third solutions are approximate, and the second and fourth are exact. The graphical method is often used to estimate the number of roots and their approximate boundaries. Solutions are more often approximate than exact.

