Expectation variance formulas. Mathematical expectation is the probability distribution of a random variable
The concept of mathematical expectation can be considered using the example of throwing a die. With each throw, the dropped points are recorded. To express them, natural values in the range 1 – 6 are used.
After a certain amount throws using simple calculations you can find the average arithmetic value dropped points.
Just like the occurrence of any of the values in the range, this value will be random.
What if you increase the number of throws several times? At large quantities throws, the arithmetic average of the points will approach a specific number, which in probability theory is called the mathematical expectation.
So, by mathematical expectation we mean the average value random variable. This indicator can also be presented as a weighted sum of probable value values.
This concept has several synonyms:
- average;
- average value;
- indicator of central tendency;
- first moment.
In other words, it is nothing more than a number around which the values of a random variable are distributed.
IN various fields human activity approaches to understanding mathematical expectation will be somewhat different.
It can be considered as:
- the average benefit obtained from making a decision, when such a decision is considered from the point of view of large number theory;
- the possible amount of winning or losing (gambling theory), calculated on average for each bet. In slang, they sound like “player’s advantage” (positive for the player) or “casino advantage” (negative for the player);
- percentage of profit received from winnings.
The expectation is not mandatory for absolutely all random variables. It is absent for those who have a discrepancy in the corresponding sum or integral.
Properties of mathematical expectation
Like any statistical parameter, the mathematical expectation has the following properties:

Basic formulas for mathematical expectation
The calculation of the mathematical expectation can be performed both for random variables characterized by both continuity (formula A) and discreteness (formula B):
- M(X)=∑i=1nxi⋅pi, where xi are the values of the random variable, pi are the probabilities:
- M(X)=∫+∞−∞f(x)⋅xdx, where f(x) is the given probability density.
Examples of calculating mathematical expectation
Example A.
Is it possible to find out the average height of the dwarves in the fairy tale about Snow White. It is known that each of the 7 dwarves had a certain height: 1.25; 0.98; 1.05; 0.71; 0.56; 0.95 and 0.81 m.
The calculation algorithm is quite simple:
- we find the sum of all values of the growth indicator (random variable):
1,25+0,98+1,05+0,71+0,56+0,95+ 0,81 = 6,31; - Divide the resulting amount by the number of gnomes:
6,31:7=0,90.
Thus, the average height of gnomes in a fairy tale is 90 cm. In other words, this is the mathematical expectation of the growth of gnomes.
Working formula - M(x)=4 0.2+6 0.3+10 0.5=6
Practical implementation of mathematical expectation
The calculation of the statistical indicator of mathematical expectation is used in various fields practical activities. First of all, we are talking about the commercial sphere. After all, Huygens’s introduction of this indicator is associated with determining the chances that can be favorable, or, on the contrary, unfavorable, for some event.
 This parameter is widely used to assess risks, especially when it comes to financial investments.
This parameter is widely used to assess risks, especially when it comes to financial investments.
Thus, in business, the calculation of mathematical expectation acts as a method for assessing risk when calculating prices.
This indicator can also be used to calculate the effectiveness of certain measures, for example, labor protection. Thanks to it, you can calculate the probability of an event occurring.
Another area of application this parameter– management. It can also be calculated during product quality control. For example, using mat. expectations, you can calculate the possible number of defective parts produced.
The mathematical expectation also turns out to be irreplaceable when carrying out statistical processing of the results obtained during scientific research results. It allows you to calculate the probability of a desired or undesirable outcome of an experiment or study depending on the level of achievement of the goal. After all, its achievement can be associated with gain and benefit, and its failure can be associated with loss or loss.
Using mathematical expectation in Forex
The practical application of this statistical parameter is possible when conducting transactions on the foreign exchange market. With its help, you can analyze the success of trade transactions. Moreover, an increase in the expectation value indicates an increase in their success.
It is also important to remember that the mathematical expectation should not be considered as the only statistical parameter used to analyze a trader’s performance. The use of several statistical parameters along with the average value increases the accuracy of the analysis significantly.
This parameter has proven itself well in monitoring observations of trading accounts. Thanks to it, a quick assessment of the work carried out on the deposit account is carried out. In cases where the trader’s activity is successful and he avoids losses, it is not recommended to use exclusively the calculation of mathematical expectation. In these cases, risks are not taken into account, which reduces the effectiveness of the analysis.
Conducted studies of traders’ tactics indicate that:
- The most effective tactics are those based on random entry;
- The least effective are tactics based on structured inputs.
Equally important in achieving positive results:
- money management tactics;
- exit strategies.
Using such an indicator as the mathematical expectation, you can predict what the profit or loss will be when investing 1 dollar. It is known that this indicator, calculated for all games practiced in the casino, is in favor of the establishment. This is what allows you to make money. In the case of a long series of games, the likelihood of a client losing money increases significantly.
Games professional players are limited to short time periods, which increases the probability of winning and reduces the risk of loss. The same pattern is observed when performing investment operations.
An investor can earn a significant amount with positive anticipation and execution. large quantity transactions over a short period of time.
Expectation can be thought of as the difference between the percentage of profit (PW) multiplied by the average profit (AW) and the probability of loss (PL) multiplied by the average loss (AL).
As an example, we can consider the following: position – 12.5 thousand dollars, portfolio – 100 thousand dollars, deposit risk – 1%. The profitability of transactions is 40% of cases with an average profit of 20%. In case of loss, the average loss is 5%. Calculating the mathematical expectation for the transaction gives a value of $625.
Random variable is a variable that, as a result of each trial, takes one thing in advance unknown value, depending on random reasons. Random variables are denoted in capitals in Latin letters: $X,\ Y,\ Z,\ \dots $ According to their type, random variables can be discrete And continuous.
Discrete random variable- this is a random variable whose values can be no more than countable, that is, either finite or countable. By countability we mean that the values of a random variable can be numbered.
Example 1 . Here are examples of discrete random variables:
a) the number of hits on the target with $n$ shots, here the possible values are $0,\ 1,\ \dots ,\ n$.
b) the number of emblems dropped when tossing a coin, here the possible values are $0,\ 1,\ \dots ,\ n$.
c) the number of ships arriving on board (a countable set of values).
d) the number of calls arriving at the PBX (countable set of values).
1. Law of probability distribution of a discrete random variable.
A discrete random variable $X$ can take values $x_1,\dots ,\ x_n$ with probabilities $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. The correspondence between these values and their probabilities is called law of distribution of a discrete random variable. As a rule, this correspondence is specified using a table, the first line of which indicates the values $x_1,\dots ,\ x_n$, and the second line contains the probabilities $p_1,\dots ,\ p_n$ corresponding to these values.
$\begin(array)(|c|c|)
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end(array)$
Example 2 . Let the random variable $X$ be the number of points rolled when tossing a die. Such a random variable $X$ can take the following values: $1,\ 2,\ 3,\ 4,\ 5,\ 6$. The probabilities of all these values are equal to $1/6$. Then the law of probability distribution of the random variable $X$:
$\begin(array)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
\hline
\end(array)$
Comment. Since in the distribution law of a discrete random variable $X$ the events $1,\ 2,\ \dots ,\ 6$ form a complete group of events, then the sum of the probabilities must be equal to one, that is, $\sum(p_i)=1$.
2. Mathematical expectation of a discrete random variable.
Expectation of a random variable sets its “central” meaning. For a discrete random variable, the mathematical expectation is calculated as the sum of the products of the values $x_1,\dots ,\ x_n$ and the probabilities $p_1,\dots ,\ p_n$ corresponding to these values, that is: $M\left(X\right)=\sum ^n_(i=1)(p_ix_i)$. In English-language literature, another notation $E\left(X\right)$ is used.
Properties of mathematical expectation$M\left(X\right)$:
- $M\left(X\right)$ is contained between the smallest and highest values random variable $X$.
- The mathematical expectation of a constant is equal to the constant itself, i.e. $M\left(C\right)=C$.
- The constant factor can be taken out of the sign of the mathematical expectation: $M\left(CX\right)=CM\left(X\right)$.
- The mathematical expectation of the sum of random variables is equal to the sum of their mathematical expectations: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
- The mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$.
Example 3 . Let's find the mathematical expectation of the random variable $X$ from example $2$.
$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\over (6))+4\cdot ((1)\over (6))+5\cdot ((1)\over (6))+6\cdot ((1 )\over (6))=3.5.$$
We can notice that $M\left(X\right)$ lies between the smallest ($1$) and largest ($6$) values of the random variable $X$.
Example 4 . It is known that the mathematical expectation of the random variable $X$ is equal to $M\left(X\right)=2$. Find the mathematical expectation of the random variable $3X+5$.
Using the above properties, we get $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\cdot 2 +5=11$.
Example 5 . It is known that the mathematical expectation of the random variable $X$ is equal to $M\left(X\right)=4$. Find the mathematical expectation of the random variable $2X-9$.
Using the above properties, we get $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\cdot 4 -9=-1$.
3. Dispersion of a discrete random variable.
Possible values of random variables with equal mathematical expectations can disperse differently around their average values. For example, in two student groups the average score for the exam in probability theory turned out to be 4, but in one group everyone turned out to be good students, and in the other group there were only C students and excellent students. Therefore, there is a need for a numerical characteristic of a random variable that would show the spread of the values of the random variable around its mathematical expectation. This characteristic is dispersion.
Variance of a discrete random variable$X$ is equal to:
$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2).\ $$
In English literature the notation $V\left(X\right),\ Var\left(X\right)$ is used. Very often the variance $D\left(X\right)$ is calculated using the formula $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\left(X \right)\right))^2$.
Dispersion properties$D\left(X\right)$:
- The variance is always greater than or equal to zero, i.e. $D\left(X\right)\ge 0$.
- The variance of the constant is zero, i.e. $D\left(C\right)=0$.
- The constant factor can be taken out of the dispersion sign provided that it is squared, i.e. $D\left(CX\right)=C^2D\left(X\right)$.
- The variance of the sum of independent random variables is equal to the sum of their variances, i.e. $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$.
- The variance of the difference between independent random variables is equal to the sum of their variances, i.e. $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$.
Example 6 . Let's calculate the variance of the random variable $X$ from example $2$.
$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2)=((1)\over (6))\cdot (\left(1-3.5\right))^2+((1)\over (6))\cdot (\left(2-3.5\right))^2+ \dots +((1)\over (6))\cdot (\left(6-3.5\right))^2=((35)\over (12))\approx 2.92.$$
Example 7 . It is known that the variance of the random variable $X$ is equal to $D\left(X\right)=2$. Find the variance of the random variable $4X+1$.
Using the above properties, we find $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0=16D\ left(X\right)=16\cdot 2=32$.
Example 8 . It is known that the variance of the random variable $X$ is equal to $D\left(X\right)=3$. Find the variance of the random variable $3-2X$.
Using the above properties, we find $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)=4D\ left(X\right)=4\cdot 3=12$.
4. Distribution function of a discrete random variable.
The method of representing a discrete random variable in the form of a distribution series is not the only one, and most importantly, it is not universal, since a continuous random variable cannot be specified using a distribution series. There is another way to represent a random variable - the distribution function.
Distribution function random variable $X$ is called a function $F\left(x\right)$, which determines the probability that the random variable $X$ will take a value less than some fixed value $x$, that is, $F\left(x\right )=P\left(X< x\right)$
Properties of the distribution function:
- $0\le F\left(x\right)\le 1$.
- The probability that the random variable $X$ will take values from the interval $\left(\alpha ;\ \beta \right)$ is equal to the difference between the values of the distribution function at the ends of this interval: $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
- $F\left(x\right)$ - non-decreasing.
- $(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \right)=1\ )$.
Example 9 . Let us find the distribution function $F\left(x\right)$ for the distribution law of the discrete random variable $X$ from example $2$.
$\begin(array)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end(array)$
If $x\le 1$, then, obviously, $F\left(x\right)=0$ (including for $x=1$ $F\left(1\right)=P\left(X< 1\right)=0$).
If $1< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.
If $2< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.
If $3< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.
If $4< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.
If $5< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.
If $x > 6$, then $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right) +P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+ 1/6+1/6=1$.
So $F(x)=\left\(\begin(matrix)
0,\ at\ x\le 1,\\
1/6,at\ 1< x\le 2,\\
1/3,\ at\ 2< x\le 3,\\
1/2,at\ 3< x\le 4,\\
2/3,\ at\ 4< x\le 5,\\
5/6,\ at\ 4< x\le 5,\\
1,\ for\ x > 6.
\end(matrix)\right.$
Expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of scattering. In many practical problems, a complete, exhaustive characteristic of a random variable - the distribution law - either cannot be obtained at all, or is not needed at all. In these cases, one is limited to an approximate description of a random variable using numerical characteristics.
The expected value is often called simply the average value of a random variable. Dispersion of a random variable is a characteristic of dispersion, the spread of a random variable around its mathematical expectation.
Expectation of a discrete random variable
Let us approach the concept of mathematical expectation, first based on the mechanical interpretation of the distribution of a discrete random variable. Let the unit mass be distributed between the points of the x-axis x1 , x 2 , ..., x n, and each material point has a corresponding mass of p1 , p 2 , ..., p n. It is required to select one point on the abscissa axis, characterizing the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, to which the abscissa of each point xi enters with a “weight” equal to the corresponding probability. The average value of the random variable obtained in this way X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:

Example 1. A win-win lottery has been organized. There are 1000 winnings, of which 400 are 10 rubles. 300 - 20 rubles each. 200 - 100 rubles each. and 100 - 200 rubles each. What medium size winnings for those who bought one ticket?
Solution. We will find the average winnings if we divide the total amount of winnings, which is 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, by 1000 (total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average winnings can be presented in the following form:
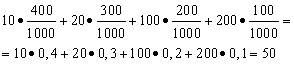
On the other hand, under these conditions, the winning size is a random variable, which can take values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average win is equal to the sum of the products of the size of the wins and the probability of receiving them.
Example 2. The publisher decided to publish new book. He plans to sell the book for 280 rubles, of which he himself will receive 200, 50 - the bookstore and 30 - the author. The table provides information about the costs of publishing a book and the probability of selling a certain number of copies of the book.
Find the publisher's expected profit.
Solution. The random variable “profit” is equal to the difference between the income from sales and the cost of costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publication is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher’s profit:
![]() .
.
Example 3. Probability of hitting with one shot p= 0.2. Determine the consumption of projectiles that provide a mathematical expectation of the number of hits equal to 5.
Solution. From the same mathematical expectation formula that we have used so far, we express x- shell consumption:
![]() .
.
Example 4. Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of a hit with each shot p = 0,4 .
Hint: find the probability of random variable values by Bernoulli's formula .
Properties of mathematical expectation
Let's consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the mathematical expectation sign:
![]()
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of a product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of a random variable X decrease (increase) by the same number WITH, then its mathematical expectation will decrease (increase) by the same number:
![]()
When you can’t limit yourself only to mathematical expectation
In most cases, only the mathematical expectation cannot sufficiently characterize a random variable.
Let the random variables X And Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:
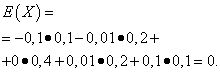
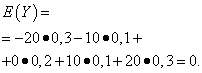
However, their distribution patterns are different. Random variable X can only take values that differ little from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average salary does not make it possible to judge specific gravity high and low paid workers. In other words, one cannot judge from the mathematical expectation what deviations from it, at least on average, are possible. To do this, you need to find the variance of the random variable.
Variance of a discrete random variable
Variance discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:
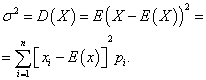
The standard deviation of a random variable X the arithmetic value of the square root of its variance is called:
![]() .
.
Example 5. Calculate variances and standard deviations of random variables X And Y, the distribution laws of which are given in the tables above.
Solution. Mathematical expectations of random variables X And Y, as found above, are equal to zero. According to the dispersion formula at E(X)=E(y)=0 we get:
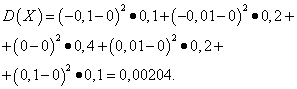
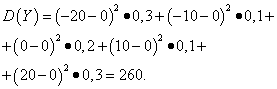
Then the standard deviations of random variables X And Y make up
![]() .
.
Thus, with the same mathematical expectations, the variance of the random variable X very small, but a random variable Y- significant. This is a consequence of differences in their distribution.
Example 6. The investor has 4 alternative investment projects. The table summarizes the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find for each alternative the mathematical expectation, variance and standard deviation.
Solution. Let us show how these values are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectations. This means that in the long run everyone has the same income. Standard deviation can be interpreted as a measure of risk - the higher it is, the greater the risk of the investment. An investor who does not want much risk will choose project 1 since it has the smallest standard deviation (0). If the investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation - project 4.
Dispersion properties
Let us present the properties of dispersion.
Property 1. The variance of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
![]() .
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
![]() ,
,
Where ![]() .
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7. It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Solution. Let us denote by p the probability with which a random variable takes a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let us derive the equation for the mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
Law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of dispersion:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then look at the solution
Example 8. Discrete random variable X takes only two values. It accepts the greater of the values 3 with probability 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9. There are 6 white and 4 black balls in the urn. 3 balls are drawn from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Solution. Random variable X can take values 0, 1, 2, 3. The corresponding probabilities can be calculated from probability multiplication rule. Law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Expectation and variance of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). Unlike a discrete random variable, whose function argument xi changes abruptly; for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its average value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If the density function of a continuous random variable is given, then it directly enters into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and their probabilities.
Let a random variable take only probability values which are respectively equal. Then the mathematical expectation of a random variable is determined by the equality
If a discrete random variable takes a countable set of possible values, then
Moreover, the mathematical expectation exists if the series on the right side of the equality converges absolutely.
Comment. From the definition it follows that the mathematical expectation of a discrete random variable is a non-random (constant) quantity.
Definition of mathematical expectation in the general case
Let us determine the mathematical expectation of a random variable whose distribution is not necessarily discrete. Let's start with the case of non-negative random variables. The idea will be to approximate such random variables using discrete ones for which the mathematical expectation has already been determined, and to set the mathematical expectation equal to the limit of the mathematical expectations of the discrete random variables that approximate it. By the way, this is a very useful general idea, which is that some characteristic is first determined for simple objects, and then for more complex objects it is determined by approximating them by simpler ones.
Lemma 1. Let there be an arbitrary non-negative random variable. Then there is a sequence of discrete random variables such that

Proof. Let us divide the semi-axis into equal length segments and determine
Then properties 1 and 2 easily follow from the definition of a random variable, and
Lemma 2. Let be a non-negative random variable and and two sequences of discrete random variables possessing properties 1-3 from Lemma 1. Then
Proof. Note that for non-negative random variables we allow
Due to property 3, it is easy to see that there is a sequence positive numbers, such that
It follows that
Using the properties of mathematical expectations for discrete random variables, we obtain
Passing to the limit at we obtain the statement of Lemma 2.
Definition 1. Let be a non-negative random variable, - a sequence of discrete random variables that have properties 1-3 from Lemma 1. The mathematical expectation of a random variable is the number
Lemma 2 guarantees that it does not depend on the choice of approximating sequence.
Let now be an arbitrary random variable. Let's define


From the definition and it easily follows that

Definition 2. The mathematical expectation of an arbitrary random variable is the number
If at least one of the numbers on the right side of this equality is finite.
Properties of mathematical expectation
Property 1. The mathematical expectation of a constant value is equal to the constant itself:
Proof. We will consider a constant as a discrete random variable that has one possible value and takes it with probability, therefore,
Remark 1. Let us define the product of a constant variable by a discrete random variable as a discrete random whose possible values are equal to the products of the constant by the possible values; the probabilities of possible values are equal to the probabilities of the corresponding possible values. For example, if the probability of a possible value is then the probability that the value will take the value is also equal
Property 2. The constant factor can be taken out of the sign of the mathematical expectation:
Proof. Let the random variable be given by the probability distribution law:
Taking into account Remark 1, we write the distribution law of the random variable
Note 2: Before moving on to to the following property, we point out that two random variables are called independent if the distribution law of one of them does not depend on what possible values the other variable took. Otherwise, the random variables are dependent. Several random variables are called mutually independent if the laws of distribution of any number of them do not depend on what possible values the remaining variables took.
Remark 3. Let us define the product of independent random variables and as a random variable whose possible values are equal to the products of each possible value by each possible value, the probabilities of the possible values of the product are equal to the products of the probabilities of the possible values of the factors. For example, if the probability of a possible value is, the probability of a possible value is then the probability of a possible value is
Property 3. The mathematical expectation of the product of two independent random variables is equal to the product of their mathematical expectations:
Proof. Let independent random variables be specified by their own probability distribution laws:
Let's compile all the values that a random variable can take. To do this, let's multiply all possible values by each possible value; As a result, we obtain and, taking into account Remark 3, we write the distribution law, assuming for simplicity that all possible values of the product are different (if this is not the case, then the proof is carried out in a similar way):
The mathematical expectation is equal to the sum of the products of all possible values and their probabilities:
Consequence. The mathematical expectation of the product of several mutually independent random variables is equal to the product of their mathematical expectations.
Property 4. The mathematical expectation of the sum of two random variables is equal to the sum of the mathematical expectations of the terms:
Proof. Let random variables and be specified by the following distribution laws:
Let's compile all possible values of a quantity. To do this, we add each possible value to each possible value; we obtain. Let us assume for simplicity that these possible values are different (if this is not the case, then the proof is carried out in a similar way), and we denote their probabilities, respectively, by and
The mathematical expectation of a value is equal to the sum of the products of possible values and their probabilities:
Let us prove that an Event that will take on the value (the probability of this event is equal) entails an event that will take on the value or (the probability of this event by the addition theorem is equal), and vice versa. Hence it follows that the equalities are proved similarly
Substituting the right-hand sides of these equalities into relation (*), we obtain
or finally
Variance and standard deviation
In practice, it is often necessary to estimate the dispersion of possible values of a random variable around its mean value. For example, in artillery it is important to know how closely the shells will fall near the target that is to be hit.
At first glance, it may seem that the easiest way to estimate dispersion is to calculate all possible deviations of a random variable and then find their average value. However, this path will not give anything, since the average value of the deviation, i.e. for any random variable is equal to zero. This property is explained by the fact that some possible deviations are positive, while others are negative; as a result of their mutual cancellation, the average deviation value is zero. These considerations indicate the advisability of replacing possible deviations with their absolute values or their squares. This is what they do in practice. True, in the case when possible deviations are replaced by absolute values, one has to operate with absolute values, which sometimes leads to serious difficulties. Therefore, most often they take a different path, i.e. calculate the average value of the squared deviation, which is called dispersion.
In the previous one, we presented a number of formulas that allow us to find the numerical characteristics of functions when the laws of distribution of arguments are known. However, in many cases, to find the numerical characteristics of functions, it is not necessary to even know the laws of distribution of arguments, but it is enough to know only some of their numerical characteristics; at the same time, we generally do without any laws of distribution. Determining the numerical characteristics of functions from given numerical characteristics of arguments is widely used in probability theory and can significantly simplify the solution of a number of problems. Most of these simplified methods relate to linear functions; however, some elementary nonlinear functions also allow a similar approach.
In the present we will present a number of theorems on the numerical characteristics of functions, which together represent a very simple apparatus for calculating these characteristics, applicable in a wide range of conditions.
1. Mathematical expectation of a non-random value
The formulated property is quite obvious; it can be proven by considering a non-random variable as a special type of random, with one possible meaning with probability one; then according to the general formula for the mathematical expectation:
![]() .
.
2. Variance of a non-random quantity
If is a non-random value, then
3. Substituting a non-random value for the sign of mathematical expectation
![]() , (10.2.1)
, (10.2.1)
that is, a non-random value can be taken out as a sign of the mathematical expectation.
Proof.
a) For discontinuous quantities
b) For continuous quantities
 .
.
4. Taking a non-random value out of the sign of dispersion and standard deviation
If is a non-random quantity, and is random, then
![]() , (10.2.2)
, (10.2.2)
that is, a non-random value can be taken out of the sign of the dispersion by squaring it.
Proof. By definition of variance
Consequence
![]() ,
,
that is, a non-random value can be taken out of the sign of the standard deviation by its absolute value. We obtain the proof by taking the square root from formula (10.2.2) and taking into account that the r.s.o. - a significantly positive value.
5. Mathematical expectation of the sum of random variables
Let us prove that for any two random variables and
that is, the mathematical expectation of the sum of two random variables is equal to the sum of their mathematical expectations.
This property is known as the theorem of addition of mathematical expectations.
Proof.
a) Let be a system of discontinuous random variables. Let us apply the general formula (10.1.6) to the sum of random variables for the mathematical expectation of a function of two arguments:
![]() .
.
Ho represents nothing more than the total probability that the quantity will take the value :
![]() ;
;
hence,
![]() .
.
We will similarly prove that
![]() ,
,
and the theorem is proven.
b) Let be a system of continuous random variables. According to formula (10.1.7)

 . (10.2.4)
. (10.2.4)
Let us transform the first of the integrals (10.2.4):

 ;
;
similarly
 ,
,
and the theorem is proven.
It should be specially noted that the theorem for adding mathematical expectations is valid for any random variables - both dependent and independent.
The theorem for adding mathematical expectations is generalized to an arbitrary number of terms:
 , (10.2.5)
, (10.2.5)
that is, the mathematical expectation of the sum of several random variables is equal to the sum of their mathematical expectations.
To prove it, it is enough to use the method of complete induction.
6. Mathematical expectation of a linear function
Consider a linear function of several random arguments:
where are non-random coefficients. Let's prove that
 , (10.2.6)
, (10.2.6)
i.e. the mathematical expectation of a linear function is equal to the same linear function of the mathematical expectations of the arguments.
Proof. Using the addition theorem of m.o. and the rule of placing a non-random quantity outside the sign of the m.o., we obtain:

 .
.
7. Dispepthis sum of random variables
The variance of the sum of two random variables is equal to the sum of their variances plus twice the correlation moment:
Proof. Let's denote
According to the theorem of addition of mathematical expectations
Let's move from random variables to the corresponding centered variables. Subtracting equality (10.2.9) term by term from equality (10.2.8), we have:
By definition of variance
![]()
Q.E.D.
Formula (10.2.7) for the variance of the sum can be generalized to any number of terms:
 ,
(10.2.10)
,
(10.2.10)
where is the correlation moment of the quantities, the sign under the sum means that the summation extends to all possible pairwise combinations of random variables ![]() .
.
The proof is similar to the previous one and follows from the formula for the square of a polynomial.
Formula (10.2.10) can be written in another form:
 , (10.2.11)
, (10.2.11)
where the double sum extends to all elements of the correlation matrix of the system of quantities ![]() , containing both correlation moments and variances.
, containing both correlation moments and variances.
If all random variables ![]() , included in the system, are uncorrelated (i.e., when ), formula (10.2.10) takes the form:
, included in the system, are uncorrelated (i.e., when ), formula (10.2.10) takes the form:
 , (10.2.12)
, (10.2.12)
that is, the variance of the sum of uncorrelated random variables is equal to the sum of the variances of the terms.
This position is known as the theorem of addition of variances.
8. Variance of a linear function
Let's consider a linear function of several random variables.
where are non-random quantities.
Let us prove that the dispersion of this linear function is expressed by the formula
 , (10.2.13)
, (10.2.13)
where is the correlation moment of the quantities , .
Proof. Let us introduce the notation:
 . (10.2.14)
. (10.2.14)
Applying formula (10.2.10) for the dispersion of the sum to the right side of expression (10.2.14) and taking into account that , we obtain:
where is the correlation moment of the quantities:
![]() .
.
Let's calculate this moment. We have:
![]() ;
;
similarly
Substituting this expression into (10.2.15), we arrive at formula (10.2.13).
In the special case when all quantities ![]() are uncorrelated, formula (10.2.13) takes the form:
are uncorrelated, formula (10.2.13) takes the form:
 , (10.2.16)
, (10.2.16)
that is, the variance of a linear function of uncorrelated random variables is equal to the sum of the products of the squares of the coefficients and the variances of the corresponding arguments.
9. Mathematical expectation of a product of random variables
The mathematical expectation of the product of two random variables is equal to the product of their mathematical expectations plus the correlation moment:
Proof. We will proceed from the definition of the correlation moment:
Let's transform this expression using the properties of mathematical expectation:
which is obviously equivalent to formula (10.2.17).
If random variables are uncorrelated, then formula (10.2.17) takes the form:
that is, the mathematical expectation of the product of two uncorrelated random variables is equal to the product of their mathematical expectations.
This position is known as the theorem of multiplication of mathematical expectations.
Formula (10.2.17) is nothing more than an expression of the second mixed central moment of the system through the second mixed initial moment and mathematical expectations:
![]() . (10.2.19)
. (10.2.19)
This expression is often used in practice when calculating the correlation moment in the same way that for one random variable the variance is often calculated through the second initial moment and the mathematical expectation.
The theorem of multiplication of mathematical expectations is generalized to an arbitrary number of factors, only in this case, for its application, it is not enough that the quantities are uncorrelated, but it is required that some higher mixed moments, the number of which depends on the number of terms in the product, vanish. These conditions are certainly satisfied if the random variables included in the product are independent. In this case
 , (10.2.20)
, (10.2.20)
that is, the mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations.
This proposition can be easily proven by complete induction.
10. Variance of the product of independent random variables
Let us prove that for independent quantities
Proof. Let's denote . By definition of variance
Since the quantities are independent, and
When independent, the quantities are also independent; hence,
,
![]()
But there is nothing more than the second initial moment of the magnitude, and, therefore, is expressed through the dispersion:
![]() ;
;
similarly
![]() .
.
Substituting these expressions into formula (10.2.22) and bringing similar terms, we arrive at formula (10.2.21).
In the case when centered random variables (variables with mathematical expectations equal to zero) are multiplied, formula (10.2.21) takes the form:
![]() , (10.2.23)
, (10.2.23)
that is, the variance of the product of independent centered random variables is equal to the product of their variances.
11. Higher moments of the sum of random variables
In some cases it is necessary to calculate the highest moments of the sum of independent random variables. Let us prove some relations related here.
1) If the quantities are independent, then
Proof.
whence, according to the theorem of multiplication of mathematical expectations
But the first central moment for any quantity equal to zero; the two middle terms vanish, and formula (10.2.24) is proven.
Relation (10.2.24) is easily generalized by induction to an arbitrary number of independent terms:
 . (10.2.25)
. (10.2.25)
2) The fourth central moment of the sum of two independent random variables is expressed by the formula
where are the variances of the quantities and .
The proof is completely similar to the previous one.
Using the method of complete induction, it is easy to prove the generalization of formula (10.2.26) to an arbitrary number of independent terms.

