What is the difference between positive and negative numbers. History of Negative Numbers

The natural numbers, their opposites and the number 0 are called integers. Positive numbers(integers and fractions), negative numbers(integers and fractions) and the number 0 form a group rational numbers.

Rational numbers are designated large Latin letter R. The number 0 refers to rational integers. We learned about natural and fractional positive numbers earlier. Let's take a closer look at negative numbers as part of rational numbers.

Negative number has been associated with the word “debt” since ancient times, while positive number can be associated with the words “availability” or “income”. This means that positive integers and fractional numbers in calculations, this is what we have, and negative integers and fractions are what constitute debt. Accordingly, the result of the calculation is the difference between the available amount and our debts.

Negative integers and fractions are written with a minus sign (“-”) in front of the number. The numerical value of a negative number is its modulus. Respectively, modulus of number is the value of a number (both positive and negative) with a plus sign. Number modulus written like this: |2|; |-2|.

To everyone rational number there is a single point corresponding to the number line. Let's look at the number axis (figure below), mark a point on it ABOUT.

Point ABOUT let's match the number 0. The number 0 serves as the boundary between positive and negative numbers: to the right of 0 - positive numbers, the value of which varies from 0 to plus infinity, and to the left of 0 - negative numbers, the value of which also varies from 0 to minus infinity.

Rule. Any number to the right of the number line is greater than the number to the left.

Based on this rule, positive numbers increase from left to right, and negative numbers decrease from right to left (at the same time, the module of a negative number increases).

Properties of numbers on the number line

Every positive number and 0 are greater than any negative number.

Every positive number is greater than 0. Every negative number is less than 0.

Every negative number is less than a positive number. A positive or negative number to the right is greater than a positive or negative number to the left on the number line.

Definition. Numbers that differ from each other only in sign are called opposite numbers.

For example, the numbers 2 and -2, 6 and -6. -10 and 10. Opposite numbers located on the number axis in opposite directions from point O, but at the same distance from it.

Fractional numbers representing ordinary or decimal, follow the same rules on the number line as integers. Of two fractions, the one to the right on the number axis is larger; negative fractions are smaller than positive fractions; every positive fraction is greater than 0; every negative fraction is less than 0.

Let's say Denis has a lot of sweets - a whole big box. First Denis ate 3 candies. Then dad gave Denis 5 candies. Then Denis gave Matvey 9 candies. Finally, mom gave Denis 6 candies. Question: Did Denis end up with more or less candy than he had at first? If more, how much more? If less, how much less?

In order not to get confused with this task, it is convenient to use one trick. Let's write out all the numbers in a row from the condition. At the same time, we will put a “+” sign in front of the numbers that indicate how much more candy Denis has gained, and a “−” sign in front of the numbers that indicate how much candy Denis has decreased. Then the whole condition will be written out very briefly:

− 3 + 5 − 9 + 6.

This entry can be read, for example, like this: “First Denis received minus three candies. Then plus five candies. Then minus nine candies. And finally, plus six sweets.” The word “minus” changes the meaning of the phrase to the exact opposite. When I say: “Denis received minus three candies,” this actually means that Denis lost three candies. The word “plus,” on the contrary, confirms the meaning of the phrase. “Denis received plus five sweets” means the same thing as simply “Denis received five sweets.”

So, first Denis received minus three candies. This means that Denis now has minus three more candies than he had at the beginning. For brevity, we can say: Denis has minus three candies.

Then Denis received plus five candies. It’s easy to figure out that Denis now has two more candies. Means,

− 3 + 5 = + 2.

Then Denis received minus nine sweets. And this is how many candies he had:

− 3 + 5 − 9 = + 2 − 9 = − 7.

Finally Denis got +6 more candies. And the total amount of candy became:

− 3 + 5 − 9 + 6 = + 2 − 9 + 6 = − 7 + 6 = − 1.

In ordinary language, this means that in the end Denis ended up with one less candy than he had at the beginning. The problem is solved.

The trick with the “+” or “−” signs is used very widely. Numbers with a “+” sign are called positive. Numbers with a “−” sign are called negative. The number 0 (zero) is neither positive nor negative, because +0 is no different from −0. Thus, we are dealing with numbers from the series

..., −5, −4, −3, −2, −1, 0, +1, +2, +3, +4, +5, ...

Such numbers are called integers. And those numbers that have no sign at all and with which we have dealt so far are called natural numbers(only zero does not apply to natural numbers).

Integers can be thought of as rungs on a ladder. The number zero is landing, located level with the street. From here you can climb up, step by step, to more high floors, or you can go down to the basement. As long as we don't need to go into the basement, we'll be fine with just natural numbers and zero. Natural numbers are essentially the same as positive integers.

Strictly speaking, an integer is not a step number, but a command to move up the stairs. For example, the number +3 means that you should go up three steps, and the number −5 means that you should go down five steps. Simply, a command is taken as the number of a step, which moves us to a given step if we start moving from the zero level.

Calculations with integers are easy to do by simply mentally jumping up or down steps - unless, of course, you need to make very large jumps. But what to do when you need to jump a hundred or more steps? After all, we won’t draw such a long staircase!

But why not? We can draw a long staircase from this long distance, at which individual steps are no longer distinguishable. Then our staircase will simply turn into one straight line. And to make it more convenient to place it on the page, let’s draw it without tilting and separately mark the position of step 0.

Let's first learn how to jump along such a straight line using the example of expressions whose values we have long been able to calculate. Let it be required to find

Strictly speaking, since we are dealing with integers, we should write

But a positive number at the beginning of a line usually does not have a “+” sign. Jumping stairs looks something like this:

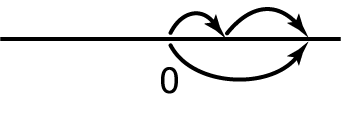
Instead of two big jumps drawn above the line (+42 and +53), you can make one jump drawn below the line, and the length of this jump, of course, is equal to

In mathematical language, these kinds of drawings are usually called diagrams. This is what the diagram looks like for our usual subtraction example:

First we made a big jump to the right, then a smaller jump to the left. As a result, we remained to the right of zero. But another situation is also possible, as, for example, in the case of the expression

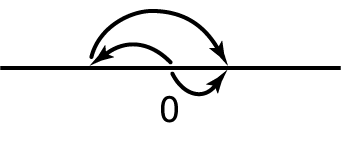
This time the jump to the right turned out to be shorter than the jump to the left: we flew over zero and ended up in the “basement” - where the steps with negative numbers are located. Let's take a closer look at our jump to the left. In total we climbed 95 steps. After we climbed 53 steps, we reached mark 0. The question is, how many steps did we climb after that? Well, of course

Thus, once we were on step 0, we went down another 42 steps, which means that we finally arrived at step number −42. So,

53 − 95 = −(95 − 53) = −42.

Likewise, by drawing diagrams, it is easy to establish that

−42 − 53 = −(42 + 53) = −95;

−95 + 53 = −(95 − 53) = −42;

and finally

−53 + 95 = 95 − 53 = 42.

Thus, we have learned to freely travel through the entire ladder of integers.

Let's now consider this problem. Denis and Matvey exchange candy wrappers. At first Denis gave Matvey 3 candy wrappers, and then took 5 candy wrappers from him. How many candy wrappers did Matvey receive in the end?

But since Denis received 2 candy wrappers, then Matvey received -2 candy wrappers. We added a minus to Denis's profit and got Matvey's profit. Our solution can be written as a single expression

−(−3 + 5) = −2.

Everything is simple here. But let's slightly modify the problem statement. Let Denis first give Matvey 5 candy wrappers, and then take 3 candy wrappers from him. The question is, again, how many candy wrappers did Matvey receive in the end?

Again, first let’s calculate Denis’s “profit”:

−5 + 3 = −2.

This means that Matvey received 2 candy wrappers. But how can we now write down our decision as a single expression? What would you add to the negative number −2 to get the positive number 2? It turns out that this time we need to assign a minus sign. Mathematicians are very fond of uniformity. They strive to ensure that solutions to similar problems are written in the form of similar expressions. In this case, the solution looks like this:

−(−5 + 3) = −(−2) = +2.

This is how mathematicians agreed: if you add a minus to a positive number, then it turns into a negative one, and if you add a minus to a negative number, then it turns into a positive one. This is very logical. After all, going down minus two steps is the same as going up plus two steps. So,

−(+2) = −2;
−(−2) = +2.

To complete the picture, we also note that

+(+2) = +2;
+(−2) = −2.

This gives us the opportunity to take a fresh look at things that have long been familiar. Let the expression be given

The meaning of this entry can be imagined in different ways. You can, in the old fashioned way, assume that the positive number +3 is subtracted from the positive number +5:

In this case +5 is called reducible, +3 - deductible, and the whole expression is difference. This is exactly what they teach in school. However, the words “reduced” and “subtracted” are not used anywhere except at school and they can be forgotten after the final test work. About this same entry we can say that the negative number −3 is added to the positive number +5:

The numbers +5 and −3 are called terms, and the whole expression is amount. There are only two terms in this sum, but, in general, the sum can consist of as many terms as you like. Likewise, the expression

can with equal right be considered as the sum of two positive numbers:

and as the difference between positive and negative numbers:

(+5) − (−3).

After we have become acquainted with integers, we definitely need to clarify the rules for opening parentheses. If there is a “+” sign in front of the brackets, then such brackets can simply be erased, and all the numbers in them retain their signs, for example:

+(+2) = +2;
+(−2) = −2;
+(−3 + 5) = −3 + 5;
+(−3 − 5) = −3 − 5;
+(5 − 3) = 5 − 3
and so on.

If there is a “−” sign in front of the brackets, then when erasing the bracket, we must also change the signs of all the numbers in it:

−(+2) = −2;
−(−2) = +2;
−(−3 + 5) = +3 − 5 = 3 − 5;
−(−3 − 5) = +3 + 5 = 3 + 5;
−(5 − 3) = −(+5 − 3) = −5 + 3;
and so on.

At the same time, it is useful to keep in mind the problem of the exchange of candy wrappers between Denis and Matvey. For example, the last line can be obtained like this. We believe that Denis first took 5 candy wrappers from Matvey, and then -3 more. In total, Denis received 5 − 3 candy wrappers, and Matvey received the same number, but with opposite sign, that is −(5 − 3) candy wrappers. But this same problem can be solved in another way, keeping in mind that every time Denis receives, Matvey gives. This means that at first Matvey received −5 candy wrappers, and then another +3, which ultimately gives −5 + 3.

Like natural numbers, integers can be compared with each other. Let us ask, for example, the question: which number is greater: −3 or −1? Let's look at the ladder with integers, and it immediately becomes clear that −1 is greater than −3, and therefore −3 is less than −1:

−1 > −3;
−3 < −1.

Now let's clarify: how much more is −1 than −3? In other words, how many steps do you need to climb to move from step −3 to step −1? The answer to this question can be written as the difference between the numbers −1 and −3:

− 1 − (−3) = −1 + 3 = 3 − 1 = 2.

Jumping up the steps, it is easy to check that this is so. Here's another interesting question: how much greater is the number 3 than the number 5? Or, which is the same thing: how many steps do you have to climb up to move from step 5 to step 3? Until recently, this question would have puzzled us. But now we can easily write out the answer:

3 − 5 = − 2.

Indeed, if we are on step 5 and go up another −2 steps, we will end up exactly on step 3.

Tasks

2.3.1. What is the meaning of the following phrases?

Denis gave dad minus three candies.

Matvey is minus two years older than Denis.

To get to our apartment, you need to go down minus two floors.

2.3.2. Do such phrases make sense?

Denis has minus three candies.

Minus two cows are grazing in the meadow.

Comment. This problem does not have a unique solution. It would not be a mistake, of course, to say that these statements are meaningless. And at the same time, they can be given a very clear meaning. Let's say Denis has a large box filled to the brim with sweets, but the contents of this box don't count. Or let’s say that two cows from the herd did not go out to graze in the meadow, but for some reason remained in the barn. It is worth keeping in mind that even the most familiar phrases can be ambiguous:

Denis has three candies.

This statement does not exclude the possibility that Denis has a huge box of candies hidden somewhere else, but those candies are simply kept silent. In the same way, when I say: “I have five rubles,” I do not mean that this is my entire fortune.

2.3.3. The grasshopper jumps up the stairs, starting from the floor where Denis's apartment is located. First he jumped 2 steps down, then 5 steps up, and finally 7 steps down. How many steps and in what direction did the grasshopper move?

2.3.4. Find the meaning of expressions:

− 6 + 10;
− 28 + 76;
etc.

− 6 + 10 = 10 − 6 = 4.

2.3.5. Find the meaning of expressions:

8 − 20;
34 − 98;
etc.

8 − 20 = − (20 − 8) = − 12.

2.3.6. Find the meaning of expressions:

− 4 − 13;
− 48 − 53;
etc.

− 4 − 13 = − (4 + 13) = − 17.

2.3.7. For the following expressions, find the values by performing calculations in the order specified by the brackets. Then open the parentheses and make sure that the meanings of the expressions remain the same. Make up problems about candies that can be solved in this way.

25 − (−10 + 4);
25 + (− 4 + 10);
etc.

25 − (− 10 + 4) = 25 − (−(10 − 4)) = 25 − (−6) = 25 + 6 = 31.

25 − (− 10 + 4) = 25 + 10 − 4 = 35 − 4 = 31.

“Denis had 25 candies. He gave dad minus ten candies, and Matvey four candies. How many candies did he have?

As a special number, it has no sign.

Examples of writing numbers: + 36, 6; − 273 ; 142. (\displaystyle +36(,)6;\ -273;\ 142.) The last number has no sign and is therefore positive.

It should be noted that plus and minus indicate sign for numbers, but not for literal variables or algebraic expressions. For example, in formulas − t ; a+b; − (a 2 + b 2) (\displaystyle -t;\ a+b;\ -(a^(2)+b^(2))) The plus and minus symbols do not specify the sign of the expression they precede, but the sign of the arithmetic operation, so the sign of the result can be anything; it is determined only after the expression has been evaluated.

In addition to arithmetic, the concept of a sign is used in other branches of mathematics, including for non-numerical mathematical objects (see below). The concept of sign is also important in those branches of physics where physical quantities are divided into two classes, conventionally called positive and negative - for example, electric charges, positive and negative feedback, various forces of attraction and repulsion.

Number sign

Positive and negative numbers

Zero is not assigned any sign, that is + 0 (\displaystyle +0) And − 0 (\displaystyle -0)- this is the same number in arithmetic. In mathematical analysis, the meaning of symbols + 0 (\displaystyle +0) And − 0 (\displaystyle -0) may vary, see about this Negative and positive zero; in computer science, computer encoding of two zeros (integer type) may differ, see Direct code.

In connection with the above, several more useful terms are introduced:

Number non-negative, if it is greater than or equal to zero.
Number negative, if it is less than or equal to zero.
Positive numbers without zero and negative numbers without zero are sometimes (to emphasize that they are non-zero) called "strictly positive" and "strictly negative", respectively.

The same terminology is sometimes used for real functions. For example, the function is called positive, if all its values are positive, non-negative, if all its values are non-negative, etc. They also say that a function is positive/negative on a given interval of its definition..

For an example of using the function, see the article Square root#Complex numbers.

Modulus (absolute value) of a number

If the number x (\displaystyle x) discard the sign, the resulting value is called module or absolute value numbers x (\displaystyle x), it is designated | x | . (\displaystyle |x|.) Examples: | 3 | = 3 ; | − 3 | = 3. (\displaystyle |3|=3;\ |-3|=3.)

For any real numbers a , b (\displaystyle a,b) the following properties hold.

Sign for non-numeric objects

Angle sign

The value of an angle on a plane is considered positive if it is measured counterclockwise, otherwise negative. Two cases of rotation are classified similarly:

rotation on a plane - for example, rotation by (–90°) occurs clockwise;
rotation in space around an oriented axis is generally considered positive if the “gimlet rule” is satisfied, otherwise it is considered negative.

Direction sign

In analytical geometry and physics, advancements along a given straight line or curve are often conventionally divided into positive and negative. Such division may depend on the formulation of the problem or on the chosen coordinate system. For example, when calculating the arc length of a curve, it is often convenient to assign a minus sign to this length in one of two possible directions.

Sign in computing

most significant bit
0	1	1	1	1	1	1	1	=	127
0	1	1	1	1	1	1	0	=	126
0	0	0	0	0	0	1	0	=	2
0	0	0	0	0	0	0	1	=	1
0	0	0	0	0	0	0	0	=	0
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	0	=	−2
1	0	0	0	0	0	0	1	=	−127
1	0	0	0	0	0	0	0	=	−128
To represent the sign of an integer, most computers use

The text of the work is posted without images and formulas.
Full version work is available in the "Work Files" tab in PDF format

Introduction

The world of numbers is very mysterious and interesting. Numbers are very important in our world. I want to learn as much as possible about the origin of numbers and their meaning in our lives. How to use them and what role do they play in our lives?

Last year in mathematics lessons we began to study the topic “Positive and Negative Numbers”. I had a question: when did negative numbers appear, in which country, which scientists studied this issue. I read on Wikipedia that a negative number is an element of the set negative numbers, which (together with zero) appeared in mathematics when expanding the set of natural numbers. The purpose of the extension is to allow the subtraction operation to be performed on any number. As a result of the expansion, a set (ring) of integers is obtained, consisting of positive (natural) numbers, negative numbers and zero.

As a result, I decided to explore the history of negative numbers.

The purpose of this work is to study the history of the emergence of negative and positive numbers.

Object of study - negative numbers and positive numbers

History of positive and negative numbers

It took people a long time to get used to negative numbers. Negative numbers seemed incomprehensible to them, they did not use them, they simply did not see much meaning in them. These numbers appeared much later than natural numbers and ordinary fractions.

The first information about negative numbers was found among Chinese mathematicians in the 2nd century. BC e. and even then, only the rules for adding and subtracting positive and negative numbers were known; the rules of multiplication and division did not apply.

In Chinese mathematics, positive quantities were called “chen”, negative quantities were called “fu”; they were portrayed different colors: “chen” - red, “fu” - black. This can be seen in the book “Arithmetic in Nine Chapters” (Author Zhang Can). This method of depiction was used in China until the middle of the 12th century, until Li Ye proposed a more convenient designation for negative numbers - the numbers that represented negative numbers were crossed out with a line diagonally from right to left.

Only in the 7th century. Indian mathematicians began to widely use negative numbers, but treated them with some mistrust. Bhaskhara directly wrote: “People do not approve of abstract negative numbers...”. This is how the Indian mathematician Brahmagupta set out the rules of addition and subtraction: “property and property is property, the sum of two debts is debt; the sum of property and zero is property; the sum of two zeros is zero... Debt, which is subtracted from zero, becomes property, and property becomes debt. If it is necessary to take away property from debt, and debt from property, then they take their sum.” “The sum of two properties is property.”

(+x) + (+y) = +(x + y)‏ (-x) + (-y) = - (x + y)‏

(-x) + (+y) = - (x - y)‏ (-x) + (+y) = +(y - x)‏

0 - (-x) = +x 0 - (+x) = -x

The Indians called positive numbers "dhana" or "sva" (property), and negative numbers "rina" or "kshaya" (debt). Indian scientists, trying to find examples of such subtraction in life, came to interpret it from the point of view of trade calculations. If a merchant has 5000 rubles. and buys goods for 3000 rubles, he has 5000 - 3000 = 2000 rubles left. If he has 3,000 rubles, but buys for 5,000 rubles, then he remains in debt for 2,000 rubles. In accordance with this, it was believed that here a subtraction of 3000 - 5000 was performed, the result being the number 2000 with a dot at the top, meaning “two thousand debt.” This interpretation was artificial; the merchant never found the amount of debt by subtracting 3000 - 5000, but always subtracted 5000 - 3000.

A little later in Ancient India and China, they guessed that instead of the words “debt of 10 yuan” they should write simply “10 yuan”, but draw these hieroglyphs with black ink. And in ancient times there were no signs “+” and “-” either for numbers or for actions.

The Greeks also did not use signs at first. The ancient Greek scientist Diophantus did not recognize negative numbers at all, and if, when solving an equation, a negative root was obtained, he discarded it as “inaccessible.” And Diophantus tried to formulate problems and compose equations in such a way as to avoid negative roots, but soon Diophantus of Alexandria began to denote subtraction with a sign.

Rules for dealing with positive and negative numbers were proposed already in the 3rd century in Egypt. The introduction of negative quantities first occurred with Diophantus. He even used special character for them. At the same time, Diophantus uses such figures of speech as “Let us add a negative to both sides,” and even formulates the rule of signs: “A negative multiplied by a negative gives a positive, while a negative multiplied by a positive gives a negative.”

In Europe, negative numbers began to be used from the 12th-13th centuries, but not until the 16th century. most scientists considered them "false", "imaginary" or "absurd", in contrast to positive numbers - "true". Positive numbers were also interpreted as “property”, and negative numbers as “debt”, “shortage”. Even the famous mathematician Blaise Pascal argued that 0 − 4 = 0, since nothing can be less than nothing. In Europe, Leonardo Fibonacci of Pisa came quite close to the idea of negative quantity at the beginning of the 13th century. At a problem-solving competition with the court mathematicians of Frederick II, Leonardo of Pisa was asked to solve a problem: it was necessary to find the capital of several individuals. Fibonacci received negative value. “This case,” said Fibonacci, “is impossible, unless we accept that one had not capital, but debt.” However, negative numbers were first used explicitly at the end of the 15th century by the French mathematician Chuquet. Author of a handwritten treatise on arithmetic and algebra, “The Science of Numbers in Three Parts.” The symbolism of Shuque is close to modern.

The recognition of negative numbers was facilitated by the work of the French mathematician, physicist and philosopher René Descartes. He proposed a geometric interpretation of positive and negative numbers - he introduced the coordinate line. (1637).

Positive numbers are represented on the number axis by points lying to the right of the beginning 0, negative numbers - to the left. The geometric interpretation of positive and negative numbers contributed to their recognition.

In 1544, the German mathematician Michael Stiefel first considered negative numbers as numbers less than zero (i.e. "less than nothing"). From this point on, negative numbers are no longer viewed as a debt, but in a completely new way. Stiefel himself wrote: “Zero is between true and absurd numbers...”

Almost simultaneously with Stiefel, the idea of negative numbers was defended by Bombelli Raffaele (about 1530-1572), an Italian mathematician and engineer who rediscovered the work of Diophantus.

Likewise, Girard considered negative numbers to be completely acceptable and useful, in particular, to indicate the lack of something.

Every physicist constantly deals with numbers: he always measures, calculates, calculates something. Everywhere in his papers there are numbers, numbers and numbers. If you look closely at the physicist’s notes, you will find that when writing numbers, he often uses the signs “+” and “-”. (For example: thermometer, depth and height scale)

Only in early XIX V. the theory of negative numbers completed its development, and “absurd numbers” received universal recognition.

Definition of the concept of number

IN modern world people constantly use numbers without even thinking about their origin. Without knowledge of the past it is impossible to understand the present. Number is one of the basic concepts of mathematics. The concept of number developed in close connection with the study of quantities; this connection continues to this day. In all branches of modern mathematics we have to consider different quantities and use numbers. Number is an abstraction used to quantify objects. Having arisen in primitive society from the needs of counting, the concept of number changed and enriched and turned into the most important mathematical concept.

Exists large number definitions of the concept “number”.

The first scientific definition of number was given by Euclid in his Elements, which he apparently inherited from his compatriot Eudoxus of Cnidus (about 408 - about 355 BC): “A unit is that in accordance with which each of the existing things are called one. A number is a set made up of units.” This is how the Russian mathematician Magnitsky defined the concept of number in his “Arithmetic” (1703). Even earlier than Euclid, Aristotle gave the following definition: “A number is a set that is measured using units.” In his “General Arithmetic” (1707), the great English physicist, mechanic, astronomer and mathematician Isaac Newton writes: “By number we mean not so much a set of units as the abstract relation of a quantity to another quantity of the same kind, taken as a unit. There are three types of numbers: integer, fractional and irrational. A whole number is something that is measured by one; fractional is a multiple of one, irrational is a number that is not commensurate with one.”

Mariupol mathematician S.F. Klyuykov also contributed to the definition of the concept of number: “Numbers are mathematical models real world invented by man for his knowledge.” He also introduced the so-called “functional numbers” into the traditional classification of numbers, meaning what is usually called functions all over the world.

Natural numbers arose when counting objects. I learned about this in 5th grade. Then I learned that the human need to measure quantities is not always expressed in whole numbers. After expanding the set of natural numbers to fractions, it became possible to divide any integer by another integer (with the exception of division by zero). Fractional numbers appeared. For a long time, subtracting an integer from another integer, when the one being subtracted is greater than the one being reduced, seemed impossible. What was interesting to me was the fact that for a long time many mathematicians did not recognize negative numbers, believing that they did not correspond to any real phenomena.

Origin of the words "plus" and "minus"

The terms come from the words plus - “more”, minus - “less”. At first, actions were denoted by the first letters p; m. Many mathematicians preferred or The origin of modern signs “+” and “-” is not entirely clear. The “+” sign probably comes from the abbreviation et, i.e. "And". However, it may have arisen from trade practice: sold measures of wine were marked “-” on the barrel, and when the stock was restored, they were crossed out, resulting in a “+” sign.

In Italy, moneylenders, when lending money, put the amount of the debt and a dash in front of the debtor’s name, like our minus, and when the debtor returned the money, they crossed it out, it turned out something like our plus.

Modern “+” signs appeared in Germany in the last decade of the 15th century. in Widmann's book, which was a manual for merchants (1489). Czech Jan Widman already wrote “+” and “-” for addition and subtraction.

A little later, the German scientist Michel Stiefel wrote "Complete Arithmetic", which was published in 1544. It contains the following entries for numbers: 0-2; 0+2; 0-5; 0+7. He called numbers of the first type “less than nothing” or “lower than nothing.” He called numbers of the second type “more than nothing” or “higher than nothing.” Of course, you understand these names, because “nothing” is 0.

Negative numbers in Egypt

However, despite such doubts, rules for operating with positive and negative numbers were proposed already in the 3rd century in Egypt. The introduction of negative quantities first occurred with Diophantus. He even used a special symbol for them (nowadays we use the minus sign for this purpose). True, scientists argue whether Diophantus’s symbol meant a negative number or simply a subtraction operation, because in Diophantus negative numbers do not occur in isolation, but only in the form of positive differences; and he considers only rational positive numbers as answers to problems. But at the same time, Diophantus uses such figures of speech as “Let us add a negative to both sides,” and even formulates the rule of signs: “A negative multiplied by a negative gives a positive, while a negative multiplied by a positive gives a negative” (that is, which is now usually formulated: “Minus by minus gives a plus, minus by plus gives a minus”).

(-) (-) = (+), (-) (+) = (-).

Negative numbers in Ancient Asia

In Chinese mathematics, positive quantities were called “chen”, negative quantities were called “fu”; they were depicted in different colors: “chen” - red, “fu” - black. This method of depiction was used in China until the middle of the 12th century, until Li Ye proposed a more convenient designation for negative numbers - the numbers that represented negative numbers were crossed out with a line diagonally from right to left. Indian scientists, trying to find examples of such subtraction in life, came to interpret it from the point of view of trade calculations.

If a merchant has 5000 rubles. and buys goods for 3000 rubles, he has 5000 - 3000 = 2000 rubles left. If he has 3,000 rubles, but buys for 5,000 rubles, then he remains in debt for 2,000 rubles. In accordance with this, it was believed that here a subtraction of 3000 - 5000 was performed, the result being the number 2000 with a dot at the top, meaning “two thousand debt.”

This interpretation was artificial; the merchant never found the amount of debt by subtracting 3000 - 5000, but always subtracted 5000 - 3000. In addition, on this basis, it was only possible to explain with a stretch the rules for adding and subtracting “numbers with dots,” but it was impossible was to explain the rules of multiplication or division.

In the 5th-6th centuries, negative numbers appeared and became very widespread in Indian mathematics. In India, negative numbers were used systematically, much as we do now. Indian mathematicians have been using negative numbers since the 7th century. n. e.: Brahmagupta formulated the rules for arithmetic operations with them. In his work we read: “property and property are property, the sum of two debts is debt; the sum of property and zero is property; the sum of two zeros is zero... Debt, which is subtracted from zero, becomes property, and property becomes debt. If it is necessary to take away property from debt, and debt from property, then they take their sum.”

The Indians called positive numbers "dhana" or "sva" (property), and negative numbers "rina" or "kshaya" (debt). However, in India there were problems with understanding and accepting negative numbers.

Negative numbers in Europe

European mathematicians did not approve of them for a long time, because the interpretation of “property-debt” caused bewilderment and doubt. In fact, how can one “add” or “subtract” property and debts, what real meaning can “multiplying” or “dividing” property by debt have? (G.I. Glazer, History of mathematics in school grades IV-VI. Moscow, Prosveshchenie, 1981)

That is why negative numbers have gained a place in mathematics with great difficulty. In Europe, Leonardo Fibonacci of Pisa came quite close to the idea of a negative quantity at the beginning of the 13th century, but negative numbers were used explicitly for the first time at the end of the 15th century by the French mathematician Chuquet. Author of a handwritten treatise on arithmetic and algebra, “The Science of Numbers in Three Parts.” Shuquet symbolism is approaching modern ones (Mathematical Encyclopedic Dictionary. M., Sov. Encyclopedia, 1988)

Modern interpretation of negative numbers

After this, Stiefel devoted his work entirely to mathematics, in which he was a self-taught genius. One of the first in Europe after Nicola Chuquet began to operate with negative numbers.

The famous French mathematician René Descartes in “Geometry” (1637) describes the geometric interpretation of positive and negative numbers; positive numbers are represented on the number axis by points lying to the right of the beginning 0, negative numbers - to the left. The geometric interpretation of positive and negative numbers led to a clearer understanding of the nature of negative numbers and contributed to their recognition.

Almost simultaneously with Stiefel, the idea of negative numbers was defended by R. Bombelli Raffaele (about 1530-1572), an Italian mathematician and engineer who rediscovered the work of Diophantus.

Bombelli and Girard, on the contrary, considered negative numbers to be quite acceptable and useful, in particular for indicating the lack of something. The modern designation for positive and negative numbers with the signs “+” and “-” was used by the German mathematician Widmann. The expression “lower than nothing” shows that Stiefel and some others mentally imagined positive and negative numbers as points on a vertical scale (like a thermometer scale). Then developed by the mathematician A. Girard, the idea of negative numbers as points on a certain line, located on the other side of zero than positive ones, turned out to be decisive in providing these numbers with citizenship rights, especially as a result of the development of the coordinate method by P. Fermat and R. Descartes .

Conclusion

In my work, I investigated the history of the emergence of negative numbers. During the research, I concluded:

Modern science encounters quantities of such a complex nature that to study them it is necessary to invent new types of numbers.

When introducing new numbers great value have two circumstances:

a) the rules of action over them must be fully defined and not lead to contradictions;

b) new number systems should contribute either to the solution of new problems or to improve already known solutions.

Currently, time has seven generally accepted levels of generalization of numbers: natural, rational, real, complex, vector, matrix and transfinite numbers. Some scientists propose to consider functions as functional numbers and expand the degree of generalization of numbers to twelve levels.

I will try to study all these sets of numbers.

Application

POEM

"Adding negative numbers and numbers with different signs»

If you really want to fold

The numbers are negative, there is no need to bother:

We need to quickly find out the sum of the modules,

Then take and add a minus sign to it.

If numbers with different signs are given,

To find their sum, we are all right there.

We can quickly select a larger module.

From it we subtract the smaller one.

The most important thing is not to forget the sign!

Which one will you put? - we want to ask

We’ll tell you a secret, it couldn’t be simpler,

Write down the sign where the module is greater in your answer.

Rules for adding positive and negative numbers

Add minus to minus,

You can get a minus.

If you add up minus, plus,

Will it turn out to be an embarrassment?!

You choose the sign of the number

Which is stronger, don't yawn!

Take them away from the modules

Make peace with all the numbers!

The rules of multiplication can be interpreted this way:

“My friend’s friend is my friend”: + ∙ + = + .

“The enemy of my enemy is my friend”: ─ ∙ ─ = +.

“The friend of my enemy is my enemy”: + ∙ ─ = ─.

“The enemy of my friend is my enemy”: ─ ∙ + = ─.

The multiplication sign is a dot, it has three signs:

Cover two of them, the third will give the answer.

For example.

How to determine the sign of the product 2∙(-3)?

Let's cover the plus and minus signs with our hands. There remains a minus sign

References

"Story ancient world", 5th grade. Kolpakov, Selunskaya.

“History of mathematics in antiquity”, E. Kolman.

"Student's Handbook." Publishing house "VES", St. Petersburg. 2003

Great mathematical encyclopedia. Yakusheva G.M. etc.

Vigasin A.A., Goder G.I., “History of the Ancient World,” 5th grade textbook, 2001.

Wikipedia. Free encyclopedia.

The emergence and development of mathematical science: Book. For the teacher. - M.: Education, 1987.

Gelfman E.G. "Positive and negative numbers", textbook on mathematics for the 6th grade, 2001.

Head ed. M. D. Aksyonova. - M.: Avanta+, 1998.

Glazer G. I. "History of mathematics at school", Moscow, "Prosveshchenie", 1981

Children's encyclopedia "I know the world", Moscow, "Enlightenment", 1995.

History of mathematics in school, grades IV-VI. G.I. Glazer, Moscow, Education, 1981.

M.: Philol. LLC "WORD": OLMA-PRESS, 2005.

Malygin K.A.

Mathematical encyclopedic dictionary. M., Sov. encyclopedia, 1988.

Nurk E.R., Telgmaa A.E. "Mathematics 6th grade", Moscow, "Enlightenment", 1989

Textbook 5th grade. Vilenkin, Zhokhov, Chesnokov, Shvartsburd.

Friedman L. M. "Studying mathematics", educational publication, 1994

E.G. Gelfman et al., Positive and negative numbers in the Buratino theater. Tutorial in mathematics for 6th grade. 3rd edition, revised, - Tomsk: Tomsk University Publishing House, 1998.

Encyclopedia for children. T.11. Mathematics

Negative numbers are located to the left of zero. For them, as for positive numbers, an order relation is defined, which allows one to compare one integer with another.

For every natural number n there is one and only one negative number, denoted -n, which complements n to zero: n + (− n) = 0 . Both numbers are called opposite for each other. Subtracting an Integer a is equivalent to adding it with its opposite: -a.

Properties of Negative Numbers

Negative numbers follow almost the same rules as natural numbers, but have some special features.

Historical sketch

Literature

Vygodsky M. Ya. Guide to elementary mathematics. - M.: AST, 2003. - ISBN 5-17-009554-6
Glazer G.I. History of mathematics in school. - M.: Education, 1964. - 376 p.

Links

Wikimedia Foundation. 2010.

See what “Negative numbers” are in other dictionaries:

Real numbers, less than zero, for example 2; 0.5; π, etc. See Number... Big Soviet encyclopedia

- (values). The result of successive additions or subtractions does not depend on the order in which these actions are performed. Eg. 10 5 + 2 = 10 +2 5. Not only the numbers 2 and 5 are rearranged here, but also the signs in front of these numbers. Agreed... ... Encyclopedic Dictionary F. Brockhaus and I.A. Efron

numbers are negative- Numbers in accounting that are written in red pencil or red ink. Topics: accounting... Technical Translator's Guide

NEGATIVE NUMBERS- numbers in accounting that are written in red pencil or red ink... Great Accounting Dictionary

The set of integers is defined as the closure of the set of natural numbers with respect to the arithmetic operations of addition (+) and subtraction (). Thus, the sum, difference and product of two integers are again integers. It consists of... ... Wikipedia

Numbers that arise naturally when counting (both in the sense of enumeration and in the sense of calculus). There are two approaches to determining natural numbers; numbers used in: listing (numbering) objects (first, second, ... ... Wikipedia

Coefficients E n in the expansion The recurrent formula for the E. number has the form (in symbolic notation, (E + 1)n + (E 1)n=0, E0 =1. In this case, E 2n+1=0, E4n are positive, E4n+2 negative integers for all n=0, 1, .; Mathematical Encyclopedia

A negative number is an element of the set of negative numbers, which (together with zero) appeared in mathematics when expanding the set of natural numbers. The purpose of the extension is to allow the subtraction operation to be performed on any number. As a result... ... Wikipedia

Arithmetic. Painting by Pinturicchio. Apartment Borgia. 1492 1495. Rome, Vatican Palaces ... Wikipedia

Hans Sebald Beham. Arithmetic. 16th century Arithmetic (ancient Greek ἀ ... Wikipedia

Books

Mathematics. 5th grade. Educational book and workshop. In 2 parts. Part 2. Positive and negative numbers,. The educational book and workshop for grade 5 are part of the teaching materials in mathematics for grades 5-6, developed by a team of authors led by E. G. Gelfman and M. A. Kholodnaya within the framework of...