お気に入りに追加

期待分散の式。数学的期待値は確率変数の確率分布です

数学的期待値の概念は、サイコロを投げる例を使用して考えることができます。投げるたびに、ドロップされたポイントが記録されます。それらを表現するには、1 ～ 6 の範囲の自然な値が使用されます。

後一定の量単純な計算を使用してスローすると、平均を見つけることができます算術値点を落とした。

範囲内の値の出現と同様に、この値もランダムになります。

投げる回数を何倍にも増やしたらどうなるでしょうか？で大量の結果、ポイントの算術平均は特定の数値に近づきます。確率論ではこれを数学的期待値と呼びます。

したがって、数学的期待とは平均値を意味します確率変数。この指標は、確率値の加重合計として表すこともできます。

この概念にはいくつかの同義語があります。

平均値。
平均値。
中心的な傾向の指標。
最初の瞬間。

言い換えれば、それは確率変数の値が分布する数値にすぎません。

でさまざまな分野人間の活動数学的期待を理解するためのアプローチは多少異なります。

それは次のように考えられます。

大数理論の観点からそのような決定を考慮した場合に、その決定を行うことで得られる平均利益。
各ベットの平均で計算された、勝ちまたは負けの可能性のある額 (ギャンブル理論)。スラングでは、「プレーヤーの利点」(プレーヤーにとってプラス) または「カジノの利点」(プレーヤーにとってマイナス) のように聞こえます。
賞金から受け取った利益の割合。

期待値は、絶対的にすべての確率変数に対して必須ではありません。対応する和や積分に矛盾がある人には存在しません。

数学的期待値の性質

他の統計パラメータと同様に、数学的期待値には次の特性があります。

数学的期待値の基本公式

数学的期待値の計算は、連続性 (式 A) と離散性 (式 B) の両方によって特徴付けられる確率変数の両方に対して実行できます。

M(X)=∑i=1nxi⋅pi、ここで xi は確率変数の値、pi は確率です。
M(X)=∫+∞−∞f(x)⋅xdx、ここで f(x) は与えられた確率密度です。

数学的期待値の計算例

例A.

白雪姫のおとぎ話に出てくる小人の平均身長を調べることはできますか。 7 人のドワーフにはそれぞれ一定の身長があることが知られています。 0.98; 1.05; 0.71; 0.56; 0.95 メートルと 0.81 メートル。

計算アルゴリズムは非常に単純です。

成長指標 (ランダム変数) のすべての値の合計を求めます。
1,25+0,98+1,05+0,71+0,56+0,95+ 0,81 = 6,31;
結果の量をノームの数で割ります。
6,31:7=0,90.

したがって、おとぎ話のノームの平均身長は 90 cm です。言い換えれば、これはノームの成長の数学的期待値です。

作動公式 - M(x)=4 0.2+6 0.3+10 0.5=6

数学的期待値の実践的実装

数学的期待値の統計的指標の計算はさまざまな分野で使用されています実践的な活動。まず第一に、商業分野について話します。結局のところ、ホイヘンスのこの指標の導入は、ある出来事に対して有利な可能性、または逆に不利な可能性を判断することに関連しています。

このパラメータは、特に金融投資のリスクを評価するために広く使用されています。
したがって、ビジネスでは、数学的期待値の計算は、価格を計算する際のリスクを評価する方法として機能します。

この指標は、労働保護などの特定の措置の有効性を計算するためにも使用できます。そのおかげで、イベントが発生する確率を計算できます。

別の応用分野このパラメータ- 管理。製品の品質管理時にも計算できます。例えばマットを使う。予想に基づいて、製造される可能性のある欠陥部品の数を計算できます。

数学的期待は、実験中に得られた結果を統計処理するときにも置き換えられないことがわかります。科学研究結果。これにより、目標の達成レベルに応じて、実験や研究の望ましい結果または望ましくない結果が生じる確率を計算できます。結局のところ、その達成は利益と利益に関連付けられ、失敗は損失と損失に関連付けられる可能性があります。

外国為替での数学的期待値の使用

外国為替市場で取引を行う場合、この統計パラメータを実際に応用することが可能です。その助けを借りて、貿易取引の成功を分析できます。さらに、期待値の増加は成功の増加を示します。

数学的期待値は、トレーダーのパフォーマンスを分析するために使用される唯一の統計パラメータとして考慮されるべきではないことを覚えておくことも重要です。平均値とともにいくつかの統計パラメータを使用すると、分析の精度が大幅に向上します。

このパラメータは、取引口座の観察を監視する際に十分に実証されています。そのおかげで、預金口座で実行された作業の迅速な評価が実行されます。トレーダーの活動が成功し、損失を回避できた場合、数学的期待値の計算のみを使用することはお勧めできません。このような場合、リスクは考慮されず、分析の有効性が低下します。

トレーダーの戦術に関する実施された調査では、次のことが示されています。

最も効果的な戦術は、ランダムなエントリーに基づいた戦術です。
最も効果が低いのは、構造化されたインプットに基づいた戦術です。

肯定的な結果を達成するには、次のことが同様に重要です。

資金管理戦術。
出口戦略。

このような指標を数学的期待値として使用すると、1 ドルを投資した場合の損益がいくらになるかを予測できます。カジノで行われるすべてのゲームについて計算されたこの指標は、カジノ施設に有利であることが知られています。これによってお金を稼ぐことができるのです。長期にわたるゲームの場合、クライアントがお金を失う可能性が大幅に高まります。

ゲームプロの選手短期間に制限されるため、勝つ確率が高まり、損失のリスクが軽減されます。投資運用を行う場合にも同じパターンが観察されます。

投資家は積極的な予測と実行によって多額の利益を得ることができます。大量短期間での取引。

期待は、利益のパーセンテージ (PW) に平均利益 (AW) を乗算したものと、損失の確率 (PL) に平均損失 (AL) を乗算した値の差として考えることができます。

例として、ポジション – 12.5 千ドル、ポートフォリオ – 100 千ドル、預金リスク – 1% を考えてみましょう。取引の収益性はケースの 40% で、平均利益は 20% です。損失が発生した場合、平均損失は 5% です。トランザクションの数学的期待値を計算すると、625 ドルの値が得られます。

確率変数各試行の結果として、1 つのことを事前に取得する変数です。未知の値、ランダムな理由に応じて。確率変数は大文字で示されますラテン文字で: $X,\ Y,\ Z,\ \dots $ 確率変数は、その種類に応じて次のようになります。離散そして 継続的な.

離散確率変数- これは、値が可算以下、つまり有限または可算のいずれかである確率変数です。可算性とは、確率変数の値に番号を付けることができることを意味します。

例1 。離散確率変数の例を次に示します。

a) $n$ ショットによるターゲットへのヒット数。ここで可能な値は、$0、\ 1、\ \dots、\ n$ です。

b) コインを投げたときにドロップされるエンブレムの数。ここで可能な値は、$0、\ 1、\ \dots、\ n$ です。

c) 到着する船の数 (可算値のセット)。

d) PBX に到着するコールの数 (可算値のセット)。

1. 離散確率変数の確率分布の法則。

離散確率変数 $X$ は、確率 $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$ を持つ値 $x_1,\dots ,\ x_n$ を取ることができます。これらの値とその確率の間の対応はと呼ばれます 離散確率変数の分布の法則。原則として、この対応関係はテーブルを使用して指定されます。テーブルの最初の行には $x_1,\dots ,\ x_n$ の値が示され、2 行目にはそれに対応する確率 $p_1,\dots ,\ p_n$ が含まれています。これらの値。

$\begin(配列)(|c|c|)
\hline
X_i & x_1 & x_2 & \ドット & x_n \\
\hline
p_i & p_1 & p_2 & \ドット & p_n \\
\hline
\end(配列)$

例 2 。確率変数 $X$ を、サイコロを投げたときに出る点の数とします。このような確率変数 $X$ は、$1、\ 2、\ 3、\ 4、\ 5、\ 6$ の値を取ることができます。これらすべての値の確率は $1/6$ に等しくなります。次に、確率変数 $X$ の確率分布の法則は次のようになります。

$\begin(配列)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline

\hline
\end(配列)$

コメント。離散確率変数 $X$ の分布法則では、イベント $1,\ 2,\ \dots ,\ 6$ がイベントの完全なグループを形成するため、確率の合計は 1、つまり $ に等しくなければなりません。 \sum(p_i)=1$。

2. 離散確率変数の数学的期待。

確率変数の期待値その「中心」の意味を設定します。離散確率変数の場合、数学的期待値は、値 $x_1,\dots ,\ x_n$ とこれらの値に対応する確率 $p_1,\dots ,\ p_n$ の積の合計として計算されます。 : $M\left(X\right)=\sum ^n_(i=1)(p_ix_i)$。英語文献では、別の表記 $E\left(X\right)$ が使用されます。

数学的期待値の性質$M\左(X\右)$:

$M\left(X\right)$ は最小値と最小値の間に含まれます。最高値確率変数 $X$。
定数の数学的期待は定数自体と等しい、つまり $M\left(C\right)=C$。
定数因数は、数学的期待値の符号から取り出すことができます: $M\left(CX\right)=CM\left(X\right)$。
確率変数の合計の数学的期待値は、それらの数学的期待値の合計に等しくなります: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$。
独立確率変数の積の数学的期待値は、数学的期待値の積に等しい: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$。

例 3 。例 $2$ から確率変数 $X$ の数学的期待値を求めてみましょう。

$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\over (6))+4\cdot ((1)\over (6))+5\cdot ((1)\over (6))+6\cdot ((1) )\over (6))=3.5.$$

$M\left(X\right)$ は、確率変数 $X$ の最小値 ($1$) と最大値 ($6$) の間にあることがわかります。

例 4 。確率変数 $X$ の数学的期待値は $M\left(X\right)=2$ に等しいことが知られています。確率変数 $3X+5$ の数学的期待値を求めます。

上記のプロパティを使用すると、 $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\ が得られます。 cdot 2 +5=$11。

例5 。確率変数 $X$ の数学的期待値は $M\left(X\right)=4$ に等しいことが知られています。確率変数 $2X-9$ の数学的期待値を求めます。

上記のプロパティを使用すると、 $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\ が得られます。 cdot 4 -9=-1$。

3. 離散確率変数の分散。

数学的期待値が等しい確率変数の可能な値は、平均値の周囲で異なる分散を示す可能性があります。たとえば、2 つの学生グループの確率論の試験の平均点は 4 でしたが、一方のグループでは全員が優秀な学生であることが判明し、もう一方のグループでは C の学生と優秀な学生のみでした。したがって、数学的期待の周囲での確率変数の値の広がりを示す、確率変数の数値特性が必要です。この特性が分散です。

離散確率変数の分散$X$ は以下に等しい:

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2).\ $$

英語文献では、$V\left(X\right),\ Var\left(X\right)$ という表記が使用されます。多くの場合、分散 $D\left(X\right)$ は、式 $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\) を使用して計算されます。 left(X \right)\right))^2$。

分散特性$D\左(X\右)$:

分散は常にゼロ以上です。つまり、 $D\left(X\right)\ge 0$。
定数の分散はゼロです。 $D\left(C\right)=0$。
定数係数は、分散符号が 2 乗である場合、分散符号から取り出すことができます。 $D\left(CX\right)=C^2D\left(X\right)$。
独立した確率変数の合計の分散は、それらの分散の合計に等しくなります。 $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$。
独立した確率変数間の差の分散は、それらの分散の合計に等しくなります。 $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$。

例6 。例 $2$ から確率変数 $X$ の分散を計算してみましょう。

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2)=((1)\over (6))\cdot (\left(1-3.5\right))^2+((1)\over (6))\cdot (\left(2-3.5\right))^2+ \dots +( (1)\over (6))\cdot (\left(6-3.5\right))^2=((35)\over (12))\約 2.92.$$

例 7 。確率変数 $X$ の分散は $D\left(X\right)=2$ に等しいことが知られています。確率変数 $4X+1$ の分散を求めます。

上記のプロパティを使用すると、 $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0= がわかります。 16D\左(X\右)=16\cdot 2=32$。

例8 。確率変数 $X$ の分散は $D\left(X\right)=3$ に等しいことが知られています。確率変数 $3-2X$ の分散を求めます。

上記のプロパティを使用すると、 $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)= がわかります。 4D\左(X\右)=4\cdot 3=12$。

4. 離散確率変数の分布関数。

離散確率変数を分布系列の形で表現する方法は唯一の方法ではありません。そして最も重要なことに、連続確率変数は分布系列を使用して指定できないため、この方法は普遍的ではありません。確率変数を表す別の方法として、分布関数があります。

分布関数確率変数 $X$ は関数 $F\left(x\right)$ と呼ばれ、確率変数 $X$ が固定値 $x$ より小さい値を取る確率、つまり $F\ を決定します。 left(x\right )=P\left(X< x\right)$

分布関数の性質:

$0\le F\left(x\right)\le 1$。
確率変数 $X$ が区間 $\left(\alpha ;\ \beta \right)$ の値を取る確率は、この両端の分布関数の値の差に等しくなります。間隔: $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
$F\left(x\right)$ - 減少しません。
$(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \right)=1\ )$。

例9 。例 $2$ からの離散確率変数 $X$ の分布法則に対する分布関数 $F\left(x\right)$ を見つけてみましょう。

$\begin(配列)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end(配列)$

$x\le 1$ の場合、明らかに $F\left(x\right)=0$ ($x=1$ の場合も $F\left(1\right)=P\left(X< 1\right)=0$).

1ドルの場合< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.

2ドルの場合< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.

3ドルなら< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.

4ドルなら< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.

5ドルなら< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.

$x > 6$ の場合、$F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right) +P\左(X=4\右)+P\左(X=5\右)+P\左(X=6\右)=1/6+1/6+1/6+1/6+ 1/6+1/6=1$。

つまり $F(x)=\left\(\begin(行列)
0,\ at\ x\le 1,\\
1/6、\1で< x\le 2,\\
1/3、\ 2< x\le 3,\\
1/2、\3で< x\le 4,\\
2/3、\ 4< x\le 5,\\
5/6、\4で< x\le 5,\\
1,\ for\ x > 6.
\end(行列)\right.$

期待値と分散は、確率変数の数値特性として最も一般的に使用されます。これらは、分布の最も重要な特徴、つまりその位置と散乱の程度を特徴付けます。多くの実際的な問題では、確率変数の完全かつ網羅的な特性 (分布法則) はまったく取得できないか、まったく必要ありません。このような場合、数値特性を使用した確率変数の近似記述に限定されます。

期待値は、単に確率変数の平均値と呼ばれることがよくあります。確率変数の分散は分散の特性の 1 つであり、数学的期待値を中心とした確率変数の広がりです。

離散確率変数の期待値

まず離散確率変数の分布の機械的解釈に基づいて、数学的期待値の概念にアプローチしてみましょう。単位質量を X 軸の点間に分布させます。 ×1 , × 2 , ..., × n、各物質点には対応する質量があります。 p1 , p 2 , ..., p n。質量を考慮して、物質点系全体の位置を特徴付ける横軸上の 1 つの点を選択する必要があります。このような点として質点系の重心を考えるのが自然である。これは確率変数の加重平均です ×、各点の横座標 ×私対応する確率に等しい「重み」でエントリーします。こうして得られた確率変数の平均値 ×は数学的期待値と呼ばれます。

離散確率変数の数学的期待値は、すべての可能な値の積とこれらの値の確率の合計です。

例1.当たる抽選会が開催されました。賞金は 1000 件あり、そのうち 400 件は 10 ルーブルです。それぞれ300〜20ルーブル。それぞれ200〜100ルーブル。それぞれ100〜200ルーブル。何中型サイズチケットを1枚購入した人に賞金はありますか？

解決。賞金総額 10*400 + 20*300 + 100*200 + 200*100 = 50,000 ルーブルを 1000 (賞金総額) で割ると、平均賞金がわかります。すると、50000/1000 = 50 ルーブルが得られます。ただし、平均賞金を計算する式は次の形式で表すことができます。

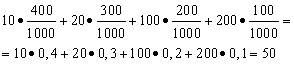
一方、これらの条件下では、賞金サイズはランダム変数であり、10、20、100、200ルーブルの値を取ることができます。確率はそれぞれ 0.4 です。 0.3; 0.2; 0.1。したがって、期待される平均勝利金は、勝利金のサイズとそれを受け取る確率の積の合計に等しくなります。

例2。出版社が出版を決めた新しい本。彼はこの本を280ルーブルで販売する予定で、そのうち200ルーブルを彼自身が受け取り、50ルーブルを書店に、30ルーブルを著者に受け取る予定だ。この表には、本の出版にかかる費用と、その本の一定部数が売れる確率に関する情報が示されています。

出版社の期待利益を求めます。

解決。確率変数「利益」は、売上からの収入と原価の差に等しくなります。たとえば、書籍が 500 部販売された場合、販売収入は 200 * 500 = 100,000 となり、出版費用は 225,000 ルーブルとなります。したがって、出版社は 125,000 ルーブルの損失に直面することになります。次の表は、確率変数 - 利益の期待値をまとめたものです。

番号	利益 ×私	確率 p私	×私 p私
500	-125000	0,20	-25000
1000	-50000	0,40	-20000
2000	100000	0,25	25000
3000	250000	0,10	25000
4000	400000	0,05	20000
合計：		1,00	25000

したがって、出版社の利益の数学的期待値が得られます。

例 3.一発で当たる確率 p= 0.2。ヒット数が 5 に等しいと数学的に予想される発射体の消費量を決定します。

解決。これまでに使用したのと同じ数学的期待公式から、次のように表されます。 ×- シェルの消費量:

例4.確率変数の数学的期待値を決定する ×各ショットでヒットする確率の場合、3 ショットでのヒット数 p = 0,4 .

ヒント: 確率変数値の確率を次のように求めます。 ベルヌーイの公式 .

数学的期待値の性質

数学的期待値の性質を考えてみましょう。

特性１．定数値の数学的期待値は、次の定数と等しくなります。

プロパティ 2。定数因数は数学的期待記号から取り出すことができます。

特性３．確率変数の合計 (差) の数学的期待値は、それらの数学的期待値の合計 (差) に等しくなります。

特性４．確率変数の積の数学的期待値は、それらの数学的期待値の積に等しいです。

特性５．確率変数のすべての値が ×同じ数字だけ減らす（増やす）との場合、その数学的期待値は同じ数値だけ減少 (増加) します。

数学的な期待だけに限定できない場合

ほとんどの場合、数学的な期待だけでは確率変数を十分に特徴付けることができません。

確率変数にしましょう ×そして Yは次の分配法則によって与えられます。

意味 ×	確率
-0,1	0,1
-0,01	0,2
0	0,4
0,01	0,2
0,1	0,1

意味 Y	確率
-20	0,3
-10	0,1
0	0,2
10	0,1
20	0,3

これらの量の数学的期待値は同じであり、ゼロに等しいです。

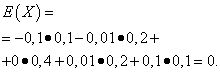
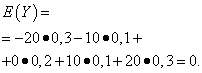
ただし、その分布パターンは異なります。確率変数 ×数学的期待とほとんど異なる値のみを取ることができ、確率変数 Y数学的な期待から大きく逸脱した値をとる可能性があります。同様の例: 平均給与だけでは判断できない比重高賃金の労働者と低賃金の労働者。言い換えれば、数学的期待値からは、少なくとも平均して、それからどのような逸脱が起こり得るかを判断することはできません。これを行うには、確率変数の分散を見つける必要があります。

離散確率変数の分散

分散離散確率変数 ×は、数学的期待値からの偏差の 2 乗の数学的期待値と呼ばれます。

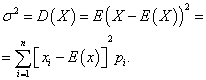
確率変数の標準偏差 ×その分散の平方根の算術値は次のように呼ばれます。

例5.確率変数の分散と標準偏差を計算する ×そして Y、その分配法則は上の表に示されています。

解決。確率変数の数学的期待 ×そして Y、上記のように、ゼロに等しい。の分散公式によると、 E(×)=E(y)=0 を得ます:

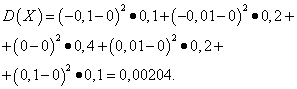
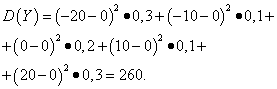
次に、確率変数の標準偏差 ×そして Y補う

したがって、同じ数学的期待値を使用すると、確率変数の分散は ×非常に小さいですが、確率変数です Y- 重要な。これは、それらの分布の違いの結果です。

例6。この投資家は 4 つのオルタナティブ投資プロジェクトを持っています。表は、これらのプロジェクトの期待利益と対応する確率をまとめたものです。

プロジェクト1	プロジェクト2	プロジェクト3	プロジェクト4
500, P=1	1000, P=0,5	500, P=0,5	500, P=0,5
	0, P=0,5	1000, P=0,25	10500, P=0,25
		0, P=0,25	9500, P=0,25

それぞれの選択肢について、数学的な期待値、分散、標準偏差を求めます。

解決。 3 番目の選択肢についてこれらの値がどのように計算されるかを示しましょう。

表には、すべての代替案について見つかった値がまとめられています。

すべての選択肢は同じ数学的期待値を持ちます。これは、長期的には誰もが同じ収入を得られることを意味します。標準偏差はリスクの尺度として解釈できます。標準偏差が高いほど、投資のリスクが大きくなります。あまりリスクを望まない投資家は、標準偏差が最小 (0) であるプロジェクト 1 を選択します。投資家が短期間でのリスクと高いリターンを好む場合、標準偏差が最も大きいプロジェクト、つまりプロジェクト 4 を選択します。

分散特性

分散の性質を示しましょう。

特性１．定数値の分散はゼロです。

プロパティ 2。定数係数は、分散符号を二乗することで分散符号から取り出すことができます。

特性３．確率変数の分散は、この値の 2 乗の数学的期待値に等しく、そこから値自体の数学的期待値の 2 乗が減算されます。

どこ .

特性４．確率変数の合計 (差) の分散は、それらの分散の合計 (差) に等しくなります。

例7。離散確率変数は ×は、-3 と 7 の 2 つの値のみを取ります。さらに、数学的期待値もわかっています。 E(×) = 4 。離散確率変数の分散を求めます。

解決。で表しましょう p確率変数が値を取る確率 ×1 = −3 。次に、値の確率 ×2 = 7 1 −になります p。数学的期待値の方程式を導き出しましょう。

E(×) = × 1 p + × 2 (1 − p) = −3p + 7(1 − p) = 4 ,

ここで確率を取得します。 p= 0.3 および 1 − p = 0,7 .

確率変数の分布の法則:

×	−3	7
p	0,3	0,7

分散のプロパティ 3 の式を使用して、この確率変数の分散を計算します。

D(×) = 2,7 + 34,3 − 16 = 21 .

確率変数の数学的期待値を自分で見つけて、その解を確認します。

例8.離散確率変数 ×は 2 つの値のみを取ります。確率 0.4 で値 3 の大きい方を受け入れます。さらに、確率変数の分散は既知です D(×) = 6 。確率変数の数学的期待値を求めます。

例9。壺の中には白玉が6個、黒玉が4個入っています。壺から3つのボールが取り出されます。描画されたボールのうちの白ボールの数は離散確率変数です ×。この確率変数の数学的な期待値と分散を求めます。

解決。確率変数 ×値は 0、1、2、3 を取ることができます。対応する確率は次から計算できます。 確率乗算ルール。確率変数の分布の法則:

×	0	1	2	3
p	1/30	3/10	1/2	1/6

したがって、この確率変数の数学的期待値は次のようになります。

M(×) = 3/10 + 1 + 1/2 = 1,8 .

与えられた確率変数の分散は次のとおりです。

D(×) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .

連続確率変数の期待値と分散

連続確率変数の場合、数学的期待値の機械的解釈は同じ意味を保持します。単位質量の質量中心が密度とともに x 軸上に連続的に分布します。 f(×）。離散確率変数とは異なり、その関数の引数は ×私突然変化する; 連続確率変数の場合、引数は連続的に変化します。ただし、連続確率変数の数学的期待は、その平均値にも関係します。

連続確率変数の数学的期待値と分散を求めるには、定積分を求める必要があります。 。連続確率変数の密度関数が与えられると、それは直接被積分関数に入ります。確率分布関数が与えられた場合、それを微分して密度関数を見つける必要があります。

連続確率変数のすべての可能な値の算術平均は、その値と呼ばれます。 数学的期待、またはで示されます。

離散確率変数の数学的期待値は、すべての可能な値とその確率の積の合計です。

確率変数がそれぞれ等しい確率値のみを取るとすると、確率変数の数学的期待値は等式によって決まります。

離散確率変数が可能な値の可算セットを取る場合、

さらに、等式の右側の系列が絶対に収束する場合、数学的期待が存在します。

コメント。この定義から、離散確率変数の数学的期待値は非ランダム (定数) 量であることがわかります。

一般的な場合の数学的期待値の定義

分布が必ずしも離散的であるとは限らない確率変数の数学的期待値を決定してみましょう。非負の確率変数の場合から始めましょう。そのアイデアは、数学的期待値がすでに決定されている離散的な確率変数を使用してそのような確率変数を近似し、その数学的期待値を、それを近似する離散的確率変数の数学的期待値の限界に等しく設定することです。ところで、これは非常に有用な一般的な考え方です。つまり、ある特性が最初に単純なオブジェクトに対して決定され、次により複雑なオブジェクトに対しては、より単純なもので近似することによって決定されるということです。

補題 1. 任意の非負の確率変数があるとします。次に、次のような一連の離散確率変数があります。

証拠。半軸を等しい長さのセグメントに分割して決定しましょう

次に、プロパティ 1 と 2 は確率変数の定義から簡単に導き出されます。

補助定理 2. を非負の確率変数とし、補助定理 1 の特性 1 ～ 3 を持つ 2 つの離散確率変数のシーケンスとする。

証拠。非負の確率変数については、次のことが許可されることに注意してください。

プロパティ 3 により、シーケンスがあることが簡単にわかります。正の数、そのような

したがって、

離散確率変数に対する数学的期待の特性を使用して、次を取得します。

極限まで通過すると、補題 2 のステートメントが得られます。

定義 1. を非負の確率変数とします。補題 1 のプロパティ 1 ～ 3 を持つ離散確率変数のシーケンスです。確率変数の数学的期待値は次の数値です。

補助定理 2 は、近似シーケンスの選択に依存しないことを保証します。

ここで、を任意の確率変数としましょう。定義しましょう

定義から、簡単に次のことがわかります。

定義 2. 任意の確率変数の数学的期待値は次の数値です。

この等式の右辺の数値の少なくとも 1 つが有限である場合。

数学的期待値の性質

プロパティ 1. 定数値の数学的期待値は、定数自体と等しくなります。

証拠。定数を、可能な値が 1 つあり、それを確率で受け取る離散確率変数として考えます。したがって、次のようになります。

注意 1. 定数変数と離散確率変数の積を、その可能な値が定数と可能な値の積に等しい離散乱数として定義しましょう。可能な値の確率は、対応する可能な値の確率に等しい。たとえば、可能な値の確率が等しい場合、その値がその値を取る確率も等しい。

特性 2. 定数因数は数学的期待値の符号から取り出すことができます。

証拠。確率変数が確率分布法則によって与えられるとします。

注 1 を考慮して、確率変数の分布則を書きます。

注 2. 次に進む前に次のプロパティに、2 つの確率変数のうちの 1 つの分布法則が、他の変数が取り得る値に依存しない場合、2 つの確率変数は独立していると呼ばれることを指摘します。それ以外の場合、確率変数は依存します。いくつかの確率変数は、それらの任意の数の分布の法則が残りの変数が取り得る値に依存しない場合、相互に独立していると呼ばれます。

注3. 独立した確率変数の積を定義しましょう。その可能な値が各可能な値と各可能な値の積に等しい確率変数として、その積の可能な値の確率は次のようになります。因子の取り得る値の確率の積。たとえば、可能な値の確率が次の場合、可能な値の確率は次のようになります。

特性 3. 2 つの独立した確率変数の積の数学的期待値は、それらの数学的期待値の積に等しい。

証拠。独立した確率変数を独自の確率分布法則によって指定するとします。

確率変数が取り得るすべての値をコンパイルするには、すべての可能な値をそれぞれの可能な値で乗算します。その結果、次の結果が得られ、注釈 3 を考慮して、分布法則を書きます。簡略化のために、製品の考えられる値はすべて異なると仮定します (そうでない場合、証明は次の方法で実行されます)。同様の方法):

数学的な期待値は、すべての可能な値とその確率の積の合計に等しくなります。

結果。いくつかの相互に独立した確率変数の積の数学的期待値は、それらの数学的期待値の積に等しくなります。

特性 4. 2 つの確率変数の合計の数学的期待値は、次の項の数学的期待値の合計に等しい。

証拠。確率変数とを次の分布法則で指定するとします。

量のすべての可能な値をコンパイルしましょう。これを行うには、可能な値をそれぞれの値に加算します。簡単にするために、これらの可能な値は異なると仮定します（そうでない場合、証明は同様の方法で実行されます）。そして、それらの確率をそれぞれとで表します。

値の数学的期待値は、可能な値とその確率の積の合計に等しくなります。

値を取るイベント (このイベントの確率は等しい) は、値 or (加法定理によるこのイベントの確率は等しい) を取るイベントを伴い、その逆も同様であることを証明しましょう。したがって、等式も同様に証明されます。

これらの等式の右辺を関係 (*) に代入すると、次のようになります。

それとも最後に

分散と標準偏差

実際には、多くの場合、確率変数の平均値の周囲の可能な値の分散を推定する必要があります。たとえば、大砲の場合、砲弾が攻撃対象の目標の近くにどれだけ近づくかを知ることが重要です。

一見すると、分散を推定する最も簡単な方法は、確率変数の考えられるすべての偏差を計算し、その平均値を見つけることであるように思えるかもしれません。ただし、偏差の平均値、つまりどの確率変数でもゼロに等しい。この特性は、考えられる偏差には正の値もあれば負の値もあるという事実によって説明されます。それらが互いに打ち消し合った結果、平均偏差値はゼロになります。これらの考慮事項は、考えられる偏差をその絶対値または二乗で置き換えることの妥当性を示しています。これが実際に彼らが行っていることです。確かに、考えられる偏差が絶対値に置き換えられる場合は、絶対値を使用して操作する必要があり、場合によっては重大な問題が発生します。したがって、ほとんどの場合、それらは異なる道をたどります。分散と呼ばれる二乗偏差の平均値を計算します。

前回では、引数の分布の法則がわかっている場合に、関数の数値的特性を見つけることができるいくつかの公式を紹介しました。ただし、多くの場合、関数の数値特性を見つけるには、引数の分布の法則を知る必要はなく、数値特性の一部だけを知るだけで十分です。同時に、私たちは通常、分配の法則を一切使用せずに行動します。引数の与えられた数値特性から関数の数値特性を決定することは、確率論で広く使用されており、多くの問題の解決を大幅に簡素化できます。これらの簡略化されたメソッドのほとんどは線形関数に関連しています。ただし、一部の初等非線形関数でも同様のアプローチが可能です。

ここでは、関数の数値的特性に関する多くの定理を提示します。これらの定理は、広範囲の条件に適用できる、これらの特性を計算するための非常に簡単な装置を示しています。

1. 非ランダム値の数学的期待

定式化された特性は非常に明白です。それは、非ランダム変数を特殊なタイプのランダムと考えることで証明できます。考えられる意味確率は 1 です。次に、数学的期待値の一般式に従います。

2. 非ランダム変数の分散

が非ランダム値の場合、

3. 数学的期待値の符号をランダムでない値に置き換える

, (10.2.1)

つまり、ランダムでない値は数学的期待の兆候として解釈できます。

証拠。

a) 不連続量の場合

b) 連続量の場合

4. 分散と標準偏差の符号をランダムでない値に置き換える

が非ランダムな量であり、ランダムである場合、

, (10.2.2)

つまり、分散の符号を 2 乗することで非ランダム値を取り出すことができます。

証拠。分散の定義によると

結果

つまり、ランダムでない値は、その絶対値によって標準偏差の符号から取り出すことができます。式 (10.2.2) から平方根を取得し、r.s.o. が次のことを考慮することによって証明が得られます。 - 著しく正の値。

5. 確率変数の合計の数学的期待

任意の 2 つの確率変数について証明してみましょう。

つまり、2 つの確率変数の合計の数学的期待値は、それらの数学的期待値の合計に等しいということです。

この性質は、数学的期待値の加算定理として知られています。

証拠。

a) を不連続確率変数の系としましょう。一般式 (10.1.6) を、2 つの引数の関数の数学的期待値の確率変数の合計に適用してみましょう。

Ho は、数量が次の値を取る確率の合計にすぎません。

;

したがって、

同様に証明します

そして定理が証明されました。

b) 連続確率変数の系としましょう。式(10.1.7)によると

. (10.2.4)

最初の積分 (10.2.4) を変換しましょう。

;

同様に

そして定理が証明されました。

数学的期待値を追加するための定理は、依存変数と独立変数の両方のあらゆる確率変数に対して有効であることに特に注意してください。

数学的期待値を追加するための定理は、任意の数の項に一般化されます。

, (10.2.5)

つまり、いくつかの確率変数の合計の数学的期待値は、それらの数学的期待値の合計に等しいということです。

それを証明するには、完全帰納法を使用するだけで十分です。

6. 一次関数の数学的期待

いくつかのランダムな引数の線形関数を考えてみましょう。

ここで、は非ランダム係数です。それを証明しましょう

, (10.2.6)

つまり、線形関数の数学的期待値は、引数の数学的期待値の同じ線形関数と等しいです。

証拠。 m.o. の加法定理を使用します。そして、非ランダムな量を m.o. の符号の外側に配置する規則により、次が得られます。

7. ディスプepこの確率変数の合計

2 つの確率変数の合計の分散は、それらの分散の合計に相関モーメントの 2 倍を加えたものに等しくなります。

証拠。と表しましょう

数学的期待値の加算定理によると

確率変数から、対応する中心変数に移りましょう。等式 (10.2.8) から等式 (10.2.9) を項ごとに減算すると、次のようになります。

分散の定義によると

Q.E.D.

合計の分散に関する式 (10.2.7) は、任意の数の項に一般化できます。

, (10.2.10)

ここで、は量の相関モーメントです。合計の下の符号は、合計が確率変数のすべての可能なペアごとの組み合わせに及ぶことを意味します。 .

証明は前の証明と同様で、多項式の 2 乗の公式に従います。

式 (10.2.10) は別の形式で書くこともできます。

, (10.2.11)

ここで、二重和は量系の相関行列のすべての要素に拡張されます。、相関モーメントと分散の両方が含まれます。

すべての確率変数の場合システムに含まれるが無相関である場合 (つまり、の場合)、式 (10.2.10) は次の形式になります。

, (10.2.12)

つまり、相関のない確率変数の合計の分散は、項の分散の合計に等しくなります。

この立場は分散加算の定理として知られています。

8. 一次関数の分散

いくつかの確率変数の一次関数を考えてみましょう。

ここで、は非ランダムな量です。

この一次関数の分散が次の式で表されることを証明しましょう。

, (10.2.13)

ここで、は量 , の相関モーメントです。

証拠。表記法を導入しましょう:

. (10.2.14)

和の分散に関する式 (10.2.10) を式 (10.2.14) の右辺に適用し、を考慮すると、次が得られます。

ここで、は量の相関モーメントです。

この瞬間を計算してみましょう。我々は持っています：

;

同様に

この式を(10.2.15)に代入すると、式(10.2.13)が得られます。

特別な場合、すべての数量相関がない場合、式 (10.2.13) は次の形式になります。

, (10.2.16)

つまり、相関のない確率変数の一次関数の分散は、係数の二乗と対応する引数の分散の積の和に等しくなります。

9. 確率変数の積の数学的期待

2 つの確率変数の積の数学的期待値は、それらの数学的期待値に相関モーメントを加えた積に等しくなります。

証拠。相関モーメントの定義から始めます。

数学的期待値の特性を使用して、この式を変形してみましょう。

これは明らかに式 (10.2.17) と等価です。

確率変数に相関がない場合、式 (10.2.17) は次の形式になります。

つまり、相関のない 2 つの確率変数の積の数学的期待値は、それらの数学的期待値の積に等しいということです。

この立場は、数学的期待の乗算定理として知られています。

式 (10.2.17) は、システムの 2 番目の混合中心モーメントを、2 番目の混合初期モーメントと数学的期待を介して表現したものにすぎません。

. (10.2.19)

この式は、1 つの確率変数の分散が 2 番目の初期モーメントと数学的期待値を通じて計算されるのと同じ方法で、相関モーメントを計算するときに実際によく使用されます。

数学的期待値の乗算の定理は、任意の数の因子に一般化されます。この場合にのみ、その適用には、量が無相関であるだけでは十分ではなく、いくつかの高次の混合モーメントが必要であり、その数は依存します。積内の項の数に応じて、消滅します。これらの条件は、積に含まれる確率変数が独立していれば必ず満たされます。この場合

, (10.2.20)