お気に入りに追加

区分関数。区分関数

チャート 区分的に与えられた 機能

ムルザリエバ T.A. 数学教師MBOU「Bor Secondary」中等学校» ボクシトゴルスク地区レニングラード地域

ターゲット：

モジュールを含むグラフを構築するための線形スプライン手法をマスターします。
簡単な状況でそれを適用することを学びます。

下 スプライン(英語のスプライン - プランク、レールに由来) は、通常、区分的に与えられた関数として理解されます。

このような関数は、オイラー以来、数学者には長い間知られていました。 (1707-1783、スイス、ドイツ、ロシアの数学者)、しかし、彼らの集中的な研究は、実際には 20 世紀半ばになってから始まりました。

1946年、アイザック・シェーンベルク (1903-1990、ルーマニアとアメリカの数学者)初めてこの用語を使いました。 1960 年の開発以来コンピューター技術コンピュータグラフィックスやモデリングでのスプラインの使用が始まりました。

1. 導入

2. 線形スプラインの定義

3. モジュールの定義

4. グラフ化

5. 実務

関数の主な目的の 1 つは、自然界で発生する実際のプロセスを記述することです。

しかし、長い間、科学者 (哲学者や自然科学者) は 2 種類のプロセスを特定してきました。 徐々に ( 継続的な ）そして けいれん的な。

遺体が地面に落ちるとき、最初にそれが起こります 継続的な増加 運転速度 そして地表に衝突した瞬間 速度が急激に変化する , なるゼロに等しい または、体が地面から「跳ねる」ときに方向 (標識) を変更します (たとえば、体がボールの場合)。

しかし、不連続なプロセスがあるため、それらを記述する手段が必要になります。この目的のために、次のような機能が導入されています。 破裂する .

a - 式 y = h(x) により、関数 g(x) と h(x) のそれぞれが x のすべての値に対して定義されており、不連続性がないと仮定します。次に、g(a) = h(a) の場合、関数 f(x) は x=a でジャンプします。 g(a) = h(a) = f(a) の場合、「結合された」関数 f には不連続性がありません。関数 g と h の両方が初等関数である場合、f は区分的初等関数と呼ばれます。 "幅=640"

このような不連続性を導入する 1 つの方法は、 次：

させて 関数 y = f(x)

で × は次の式で定義されます y = g(x)、

そしていつ ザ - 式 y = h(x)、 そして検討します それぞれの機能が g(x) そして h(x) は x のすべての値に対して定義されており、不連続性はありません。

それから , もし g(a) = h(a)、 それから関数 f(x) にあります x=a ジャンプ;

もし g(a) = h(a) = f(a)、 次に「結合」関数 f 休憩はありません。両方機能する場合 g そして h 小学校、 それ f が呼ばれます 区分的に初級。

連続関数のグラフ

関数をグラフ化します。

Y = |X-1| +1

X=1 – 式の変化点

言葉 「モジュール」ラテン語で「測定」を意味する「modulus」に由来します。

数値の係数 あ呼ばれた距離 (単一セグメントで) 原点から点 A ( A) .

この定義により明らかになるのは、幾何学的な意味モジュール。

モジュール (絶対値) 実数あ同じ番号が呼ばれますあ≥ 0、および反対の数字 -A、もし

0 または x=0 y = -3x -2 at x "width="640"

関数をグラフ化する y = 3|x|-2。

係数の定義により、x0 または x=0 で 3x – 2 となります。

-3x -2 で x

x n) "幅="640"

. x を与えましょう 1 × 2 × n – 区分的初等関数における式の変化点。

すべての x に対して定義された関数 f が各区間で線形である場合、区分的線形と呼ばれます。

さらに、調整条件は満たされます。つまり、式を変更する時点で、関数は中断されません。

連続区分線形関数 呼ばれた リニアスプライン . 彼女 スケジュール がある 2 つの無限の極端なリンクを持つポリライン – 左 (値 x に対応) n ）そしてそのとおりです ( 対応する値 x x n )

区分的初等関数は 3 つ以上の式で定義できます

スケジュール - 破線 2 つの無限の極端なリンク - 左 (x1)。

Y=|x| - |x – 1|

式の変更点: x=0 および x=1。

Y(0)=-1、y(1)=1。

区分的一次関数のグラフをプロットすると便利です。 ポインティング 座標平面上で 破線の頂点。

建物を建てるだけでなく、 n 頂点は次のとおりです 建てる また 2点 : 頂点の左に 1 つ あ 1 ( × 1; y ( × 1))、もう一方 - 上部の右側 アン ( xn ; y ( xn )).

不連続の区分的線形関数は、二項式の係数の線形結合として表すことができないことに注意してください。 .

関数をグラフ化する y = x+ |x -2| - |X|。

連続区分線形関数は線形スプラインと呼ばれます

1.計算式変更のポイント：X-2=0、 X=2 ; X=0

2. テーブルを作成しましょう:

U( 0 )= 0+|0-2|-|0|=0+2-0= 2 ;

y( 2 )=2+|2-2|-|2|=2+0-2= 0 ;

で (-1 )= -1+|-1-2| - |-1|= -1+3-1= 1 ;

y( 3 )=3+|3-2| - |3|=3+1-3= 1 .

関数 y = |x+1| のグラフを作成します。 +|x| – |x -2|。

1 .式を変更する際のポイント:

x+1=0、 x=-1 ;

x=0 ; x-2=0、 x=2。

2 . 表を作ってみましょう:

y(-2)=|-2+1|+|-2|-|-2-2|=1+2-4=-1;

y(-1)=|-1+1|+|-1|-|-1-2|=0+1-3=-2;

y(0)=1+0-2=-1;

y(2)=|2+1|+|2|-|2-2|=3+2-0=5;

y(3)=|3+1|+|3|-|3-2|=4+3-1=6。

|x – 1| = |x + 3|

方程式を解きます。

解決。 関数 y = |x -1| を考えてみましょう。 - |x +3|

/線形スプライン法を使用して関数のグラフを作成しましょう/

式の変更点:

x -1 = 0、x = 1; x + 3 =0、x = - 3。

2. テーブルを作成しましょう:

y(- 4) =|- 4–1| - |- 4+3| =|- 5| - | -1| = 5-1=4;

y( -3 )=|- 3-1| - |-3+3|=|-4| = 4;

y( 1 )=|1-1| - |1+3| = - 4 ;

y(-1) = 0。

y(2)=|2-1| - |2+3|=1 – 5 = - 4。

答え: -1。

1. 線形スプライン法を使用して区分的線形関数のグラフを作成します。

y = |x – 3| + |x|;

1). 式の変更点:

2). 表を作ってみましょう:

2. 教材「Live Mathematics」を使って関数グラフを作成する »

A) y = |2x – 4| + |x +1|

1) 式の変更点:

2) y() =

B) 関数グラフを作成し、パターンを確立する :

a) y = |x – 4| b) y = |x| +1

y = |x + 3| y = |x| - 3

y = |x – 3| y = |x| - 5

y = |x + 4| y = |x| +4

ツールバーの点、線、矢印ツールを使用します。

1. 「チャート」メニュー。

2. 「グラフの作成」タブ。

.3。「電卓」ウィンドウに数式を入力します。

関数をグラフ化します。

1) Y = 2x + 4

1. コジナ M.E. 数学。 8 ～ 9 年生: 選択コースのコレクション。 – ヴォルゴグラード: 教師、2006 年。

2. Yu. N. マカリチェフ、N. G. ミンデュク、K. I. ネシュコフ、S. B. スヴォロワ。代数: 教科書。 7年生向け。一般教養機関/編 S.A.テリャコフスキー。 – 第 17 版 – M.: 教育、2011

3. Yu. N. マカリチェフ、N. G. ミンデュク、K. I. ネシュコフ、S. B. スヴォロワ。代数: 教科書。 8年生向け。一般教養機関/編 S.A.テリャコフスキー。 – 第 17 版 – M.: 教育、2011

4. ウィキペディアは無料の百科事典です

http://ru.wikipedia.org/wiki/スプライン

7
ミキチュク Zh.N 教師による 9A 年生の代数の授業市立学校法人「中等教育学校第23校」2007/03/19レッスンのトピック: 「区分的に定義された関数」 目標:

論理的思考

言論文化

トピックを一般化した結果、学生は次のことを行う必要があります。知る：

区分的に与えられた関数の概念。各種関数の公式と対応する名称とグラフのイメージ。次のことができるようになります:

区分的に与えられた関数のグラフを構築します。チャートを読んでください。グラフを使用して分析的に関数を定義します。

レッスンの進行状況

I. 組織的および心理的瞬間。 D.K. Fadeev の言葉でレッスンを始めましょう。「どんな問題を解決しても、最後には幸せな瞬間が待っています。成功したという喜びの感情が、私たちのレッスンで真の確信をもたらします。」 II. 宿題のチェック。 いつものように d/z の確認から授業を始めましょう - 区分関数の定義と関数の学習計画を繰り返します。ボード上であなたが考え出した区分関数のグラフを描きます (図 1、2、3)2)。カード.№1。関数のプロパティを調べる順序を整理します。

凸面。偶数、奇数。範囲; 制限; 単調; 連続; 関数の最大値と最小値。定義のドメイン。 No. 2. 関数のグラフを概略的に描きます。

A) y = kx + b、k0; B) y = kx, k0;

B) y = 、k0。

3).口頭での仕事。

– 2分どの関数が区分的に呼び出されますか?

区分関数は、異なる間隔で異なる数式によって定義される関数です。図 1、2、3 に示されている区分関数はどのような関数で構成されていますか? 他にどのような関数名を知っていますか? 対応する関数のグラフは何と呼ばれますか? 図4に示した図は何かの関数のグラフでしょうか？なぜ？答え： 4) いや、だって関数の定義により、独立変数 x の各値は従属変数 y の単一の値に関連付けられます。自制心 - 3 分提案されたグラフと関数を定義する対応する式から、正しいものを選択してください。受け取った回答の文字からおなじみの単語を作成してください。答え: グラフィック人生、科学、日常生活のどこで、「グラフィック」という言葉を目にすることがありますか? - 体積と圧力の関係のグラフ。ボリュームなどのさまざまな情報を提示する工業生産 V サラトフ地方.このグラフを使用すると、各年の生産量の減少と増加を追跡できます。 - どの関数グラフがこの情報を表しているかを示します。レッスンのトピック:答え: 区分関数ターゲット：Ⅲ．トピックのメッセージ、レッスンの目的。

「区分的に定義された関数」- 区分的に与えられた関数の例を使用して、関数を学習するための計画を思い出してください。 区分的に与えられた関数を構築するステップを繰り返します。非標準的な問題を解決するときに一般化された知識を適用します。
IV. 以前に取得した知識を更新します。私たちが初めて関数の概念に出会ったのは、中学 1 年の線形依存性の学習でした。実際のプロセスをモデル化するという観点から見ると、この依存関係は一様なプロセスに対応します。例: 時間 t の間の一定の速度での歩行者の移動。式: s =vt、グラフ – 第 1 四半期に位置する線分。 8年生の主なテーマは、

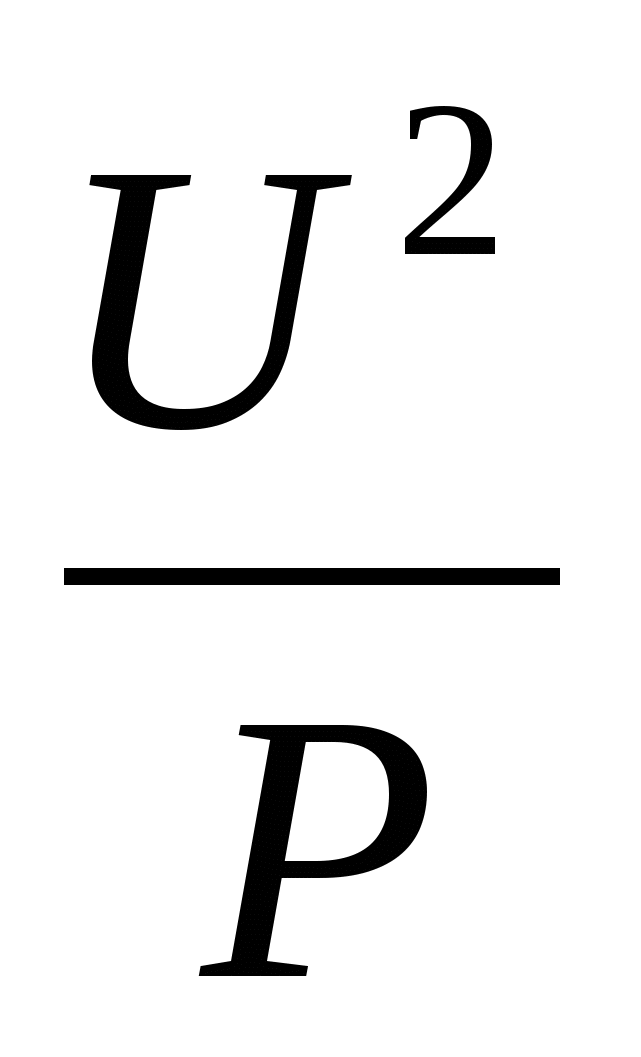二次関数
例: 9 年生で学習した、一定の電力 (P) と変化する電圧 (U) での加熱されたランプの抵抗 (R) を求める式。式R = 、グラフは第 1 四半期に位置する放物線の枝です。全体を通して 3年関数に関する知識が深まり、研究される関数の数が増え、グラフに頼らなければならない解決タスクのセットが拡張されました... -方程式を解く。- 連立方程式を解く。- 不平等を解決する。 関数の性質を学ぶ、またはグラフを読むというタスクの種類を思い出してみましょう。教科書に戻りましょう。 65 ページ、No.250 の図 20a。エクササイズ：関数のグラフを読んでください。関数を研究する手順は私たちの前にあります。 1. 定義域 – (-∞; +∞)2. 偶数、奇数 - 偶数でも奇数でもない3. 単調性 - 増加 [-3; +∞)、減少します[-5;-3]、定数 (-∞; -5];4. 境界 – 下からの制限5. 関数の最大値と最小値 – y max = 0、y max – は存在しません。6. 連続性 - 定義領域全体にわたって連続的であること。7. 値の範囲は下にも上にも凸です (-∞; -5] および [-2; +∞)。VI. 新しいレベルでの知識の再生産。 区分的に与えられた関数のグラフの作成と学習は、代数試験の第 2 部の関数セクションで扱われ、4 点と 6 点で評価されることはご存知でしょう。ページ 119 - No. 4.19-1) に移りましょう。解決策: 1).y = - x, - 二次関数、グラフ - 放物線、下向きの分岐 (a = -1、a 0)。 x -2 -1 0 1 2 y -4 -1 0 1 4 2) y = 3x – 10、 - 一次関数、グラフ - 直線いくつかの値の表を作成しましょう×3

3 y 0 -1 3) y= -3x -10、 - 一次関数、グラフ - 直線いくつかの値の表を作成しましょう x -3 -3 y 0 -1 4) 1 つの座標系で関数のグラフを作成し、所定の間隔でグラフの一部を選択してみましょう。
グラフから、x のどの値で関数の値が非負であるかを見つけてみましょう。答え: f(x)  0 at x = 0 および at

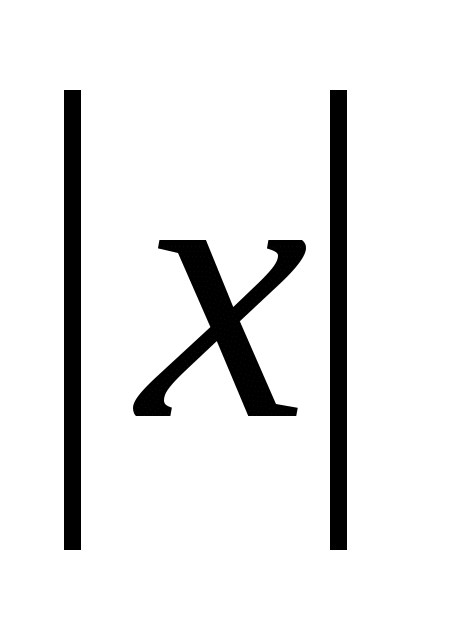 3 VII. 非標準的なタスクに取り組む。 No. 4.29-1)、121 ページ。解決： 1) 直線 (左) y = kx + b は点 (-4;0) と (-2;2) を通過します。これは、-4 k + b = 0、-2 k + b = 2 を意味します。

k = 1、b = 4、y = x+4。答え: x +4、x≠ -2 の場合 y = -2 の場合 ×￡3×の場合は3  3
VIII.知識の管理。 それでは、簡単にまとめてみましょう。レッスンで何を繰り返しましたか? 関数の学習の計画、区分関数のグラフを作成する手順、関数を分析的に指定します。この教材をどのように習得したかを確認してみましょう。「4」～「5」、「3」のテスト IオプションNo.U

2 1 -1 -1 1 X

D(f) = 、で上に凸、で下に凸、で上と下に凸、 ________ で減少 ____________ による境界はまったく存在せず、せいぜい =_____ 定義領域全体で連続 E(f) = ____________ 両方下に凸定義領域全体まで

自然界で発生する実際のプロセスは、関数を使用して説明できます。したがって、互いに反対する 2 つの主要なタイプのプロセスを区別できます。これらは次のとおりです。 徐々にまたは 継続的なそして けいれん性の(例としては、ボールが落ちて跳ね返る場合があります)。しかし、不連続なプロセスがある場合には、特別な手段それらを説明します。この目的のために、不連続性とジャンプを持つ関数が導入されます。つまり、数直線のさまざまなセクションで関数が次のように動作します。さまざまな法律したがって、異なる式で与えられます。不連続点と除去可能な不連続性の概念が導入されます。

引数の値に応じて、いくつかの数式で定義された関数をすでに見つけたことがあるでしょう。たとえば、次のとおりです。

y = (x – 3、x > -3 の場合;
(-(x – 3)、x で< -3.

このような関数は呼び出されます 区分的にまたは 区分的に指定された。数直線のセクションさまざまな公式タスク、と呼びましょう コンポーネント定義のドメイン。すべてのコンポーネントの和集合が区分関数の定義領域です。関数の定義領域をコンポーネントに分割するこれらの点は、と呼ばれます。 境界点。定義領域の各コンポーネントで区分関数を定義する式は、と呼ばれます。 受信関数。区分的に与えられた関数のグラフは、各分割間隔で構築されたグラフの一部を結合することによって取得されます。

演習。

区分関数のグラフを作成します。

1) (-3、-4 ≤ x< 0,
f(x) = (0、x = 0 の場合、
(1、0時< x ≤ 5.

最初の関数のグラフは、点 y = -3 を通過する直線です。座標 (-4; -3) の点から始まり、座標 (0; -3) の点まで x 軸と平行に進みます。 2 番目の関数のグラフは、座標 (0; 0) の点です。 3 番目のグラフは最初のグラフと似ています。これは点 y = 1 を通過する直線ですが、すでに Ox 軸に沿った 0 から 5 の領域内にあります。

答え: 図 1。

2) (x ≤ -4 の場合は 3、
f(x) = (|x 2 – 4|x| + 3|、-4 の場合< x ≤ 4,
(x > 4 の場合、3 – (x – 4) 2。

各関数を個別に検討して、グラフを作成してみましょう。

したがって、f(x) = 3 は Ox 軸に平行な直線ですが、x ≤ -4 の領域でのみ描画する必要があります。

関数 f(x) = |x 2 – 4|x| のグラフ + 3| は、放物線 y = x 2 – 4x + 3 から取得できます。グラフを作成したら、図の Ox 軸より上の部分は変更せず、横軸より下の部分を相対的に対称に表示する必要があります。牛軸に。次に、グラフの部分を対称的に表示します。
負の x の場合、Oy 軸に対して x ≥ 0。すべての変換の結果として得られたグラフを、横軸に沿った -4 から 4 までの領域のみに残します。

3 番目の関数のグラフは、枝が下に向いた放物線であり、頂点は座標 (4; 3) の点にあります。 x > 4 の領域のみに描画します。

答え: 図 2。

3) (8 – (x + 6) 2、x ≤ -6 の場合、
f(x) = (|x 2 – 6|x| + 8| (-6 ≤ x の場合)< 5,
(x ≥ 5 の場合は 3。

提案された区分的与えられた関数の構築は、前の段落と同様です。ここで、最初の 2 つの関数のグラフは放物線の変換から得られ、3 番目の関数のグラフは Ox に平行な直線です。

答え: 図 3。

4) 関数 y = x – |x| をグラフ化します。 + (x – 1 – |x|/x) 2 .

解決。この関数の範囲はすべてです実数、ゼロを除く。モジュールを展開してみましょう。これを行うには、次の 2 つのケースを考えてみましょう。

1) x > 0 の場合、y = x – x + (x – 1 – 1) 2 = (x – 2) 2 が得られます。

2) x で< 0 получим y = x + x + (x – 1 + 1) 2 = 2x + x 2 .

したがって、区分的に定義された関数が得られます。

y = ((x – 2) 2、x > 0 の場合;
( x 2 + 2x、x で< 0.

両方の関数のグラフは放物線であり、その枝は上向きです。

答え: 図 4。

5) 関数 y = (x + |x|/x – 1) のグラフを描きます。 2.

解決。

関数の定義域がゼロを除くすべての実数であることが簡単にわかります。モジュールを展開した後、区分的に指定された関数を取得します。

1) x > 0 の場合、 y = (x + 1 – 1) 2 = x 2 が得られます。

2) x で< 0 получим y = (x – 1 – 1) 2 = (x – 2) 2 .

書き直してみましょう。

y = (x 2、x > 0 の場合;
((x – 2) 2 、x で< 0.

これらの関数のグラフは放物線です。

答え: 図 5。

6) 座標平面上のグラフが任意の直線と共通点を持つ関数はあるでしょうか?

解決。

はい、存在します。

例としては、関数 f(x) = x 3 があります。実際、立方放物線のグラフは点 (a; a 3) で垂直線 x = a と交差します。ここで、直線が方程式 y = kx + b によって与えられるとします。次に、方程式
x 3 – kx – b = 0 には実数根 x 0 があります (奇数次の多項式には常に少なくとも 1 つの実数根があるため)。したがって、関数のグラフは、たとえば点 (x 0; x 0 3) で直線 y = kx + b と交差します。

ウェブサイトのコンテンツの全部または一部をコピーする場合は、ソースへのリンクが必要です。

市立予算教育機関

第13中学校

「区分関数」

サポゴワ・ヴァレンティーナと

ドンスカヤ・アレクサンドラ

ヘッドコンサルタント:

ベルツク

1. 主な目標と目的の決定。

2. アンケート。

2.1. 作品の関連性の判断

2.2. 実用的な意義。

3. 機能の歴史。

4. 一般的な特性。

5. 機能の指定方法。

6. 構築アルゴリズム。

8. 使用された文献。

1. 主な目標と目的の決定。

ターゲット：

区分関数を解く方法を見つけ、これに基づいて関数を構築するためのアルゴリズムを作成します。

タスク:

知りましょう一般的な概念区分関数について。

「関数」という用語の歴史を調べてみましょう。

アンケートを実施する。

区分関数を指定する方法を特定します。

構築のためのアルゴリズムを作成します。

2. アンケート。

区分関数を構築する能力について高校生を対象に調査が実施されました。回答者数は合計 54 名でした。そのうち 6% は作業を完全に完了しました。 28% は作業を完了できましたが、いくつかのエラーがありました。 62% は多少の試みはしたものの作業を完了できず、残りの 4% はまったく作業を開始しませんでした。

この調査から、プログラムを受講している私たちの学校の学生は十分な知識ベースを持っていないと結論付けることができます。これは、著者が注意を払っていないためです。特別な注意この種のタスクの場合。このことから、私たちの仕事の関連性と実際的な重要性がわかります。

2.1. 作品の関連性を判断する。

分析関数の割り当て

関数 %%y = f(x), x \in X%% が与えられます 明示的な分析方法で、この関数の値 %%f(x)%% を取得するために、引数 %%x%% を使用して実行する必要がある数学的演算のシーケンスを示す数式が与えられた場合。

例

%% y = 2 x^2 + 3x + 5, x \in \mathbb(R)%%;
%% y = \frac(1)(x - 5), x \neq 5%%;
%% y = \sqrt(x), x \geq 0%%。

したがって、たとえば、物理学では、均一に加速された直線運動の場合、物体の速度は式 %%v = v_0 + a t%% と、物体の %%s%% を均一に動かすための式によって決まります。加速された動き%%0%% から %%t%% までの時間間隔は、%% s = s_0 + v_0 t + \frac(a t^2)(2) %% のように記述されます。

区分的に定義された関数

問題の関数は、関数の引数が変化する定義領域の異なる部分で動作する複数の式で指定できる場合があります。例: $$ y = \begin(cases) x ^ 2,~ if~x< 0, \\ \sqrt{x},~ если~x \geq 0. \end{cases} $$

このタイプの関数は時々呼び出されます。複合または 区分的に指定された。このような関数の例は、%%y = |x|%% です。

機能ドメイン

関数が数式を使用した明示的な分析方法で指定されているが、集合 %%D%% の形式で関数の定義領域が指定されていない場合、%%D%% は常に集合を意味します。引数 %%x%% の値のうち、この式理にかなっています。したがって、関数 %%y = x^2%% の定義域は、引数 %%x%% であるため、集合 %%D = \mathbb(R) = (-\infty, +\infty)%% になります。任意の値を取ることができます 数直線。そして、関数 %%y = \frac(1)(\sqrt(1 - x^2))%% の定義域は、不等式 %%1 - を満たす値のセット %%x%% になります。 x^2 > 0%%、t .e. %%D = (-1, 1)%%。

関数を分析的に明示的に指定する利点

関数を指定する明示的な分析方法は非常にコンパクトで (一般に、式はほとんどスペースを占有しません)、再現が容易で (式を書くのは難しくありません)、数学的な演算や変換を実行するのに最適であることに注意してください。機能について。

これらの演算の一部 (加算、乗算など) は、以下のことからよく知られています。通学コース数学、その他（微分、積分）は今後勉強していきます。ただし、引数に対する関数の依存関係の性質が必ずしも明確であるとは限らず、関数の値を見つけるために (必要な場合) 面倒な計算が必要になる場合があるため、この方法は必ずしも明確ではありません。

暗黙的な関数の割り当て

関数 %%y = f(x)%% が定義されました 暗黙的な分析方法で、関係 $$F(x,y) = 0 が与えられた場合、関数 %%y%% と引数 %%x の値を接続する ~~~~~~~~~~(1)$$ %%。引数の値を指定する場合、%%x%% の特定の値に対応する %%y%% の値を見つけるには、%% について方程式 %%(1)%% を解く必要があります。この特定の値 %%x%% での y%%。

値 %%x%% を指定すると、方程式 %%(1)%% には解がないか、複数の解がある可能性があります。最初のケースでは、指定された値 %%x%% は暗黙的に指定された関数の定義のドメインに属しません。2 番目のケースでは、指定された値 %%x%% は、 多値関数、これは、特定の引数値に対して複数の意味を持ちます。

方程式 %%(1)%% が %%y = f(x)%% に関して明示的に解決できる場合、同じ関数が得られますが、すでに明示的な分析方法で指定されていることに注意してください。したがって、方程式 %%x + y^5 - 1 = 0%%

%%y = \sqrt(1 - x)%% は同じ関数を定義します。

パラメトリック関数仕様

%%x%% に対する %%y%% の依存関係が直接与えられていないが、代わりに、第 3 の補助変数 %%t%% に対する両方の変数 %%x%% と %%y%% の依存関係が与えられている場合形で

$$ \begin(cases) x = \varphi(t),\\ y = \psi(t), \end(cases) ~~~t \in T \subseteq \mathbb(R), ~~~~~ ~~~~~(2) $$彼らが話していること パラメトリック機能の指定方法。

この場合、補助変数 %%t%% はパラメータと呼ばれます。

方程式 %%(2)%% からパラメーター %%t%% を削除できる場合は、%%x%% に対する %%y%% の明示的または暗黙的な分析依存性によって定義される関数に到達します。。たとえば、関係 $$ \begin(cases) x = 2 t + 5, \\ y = 4 t + 12, \end(cases), ~~~t \in \mathbb(R), $$ 以外から% パラメータ %t%% については、%%xOy%% 平面内の直線を定義する依存関係 %%y = 2 x + 2%% が得られます。

グラフィック手法

例グラフィックタスク機能

上記の例は、関数を指定する分析方法がその関数に対応していることを示しています。 グラフィック画像、これは関数を記述する便利で視覚的な形式と考えることができます。時々使用される グラフィックメソッド %%x%% に対する %%y%% の依存関係が %%xOy%% 平面上の線で指定されている場合の関数の指定。ただし、すべての明瞭さにもかかわらず、引数の値と対応する関数の値はグラフから近似的にしか取得できないため、精度が失われます。結果として生じる誤差は、グラフ上の個々の点の横座標と縦座標の測定のスケールと精度によって異なります。以下では、関数グラフに関数の動作を説明する役割のみを割り当て、関数の主な特徴を反映するグラフの「スケッチ」の構築に限定します。